7．在半径为R的球内有一内接正三棱锥，它的底面三个顶点恰好都在同一个大圆上，一个动点从三棱锥的一个顶点出发沿球面运动，经过其余三点后返回，则经过的最短路程是________．

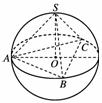[解析]　沿球面距离运动其路程最短，

+++＝2(+)

＝2＝πR.

[答案]　πR

6．球的直径为d，体积为V_球，一正方体的棱长为a，体积为V_正，若它们的表面积相同，则有(　)

A．d＞a，V_球＞V_正　 　　　　　　　　　　　　　　 B．d＞a，V_球＜V_正

C．d＜a，V_球＞V_正　 　　　　　　　　　　　　　　 D．d＜a，V_球＜V_正

[解析]　由于球的体积为πR³＝V_球，表面积为4πR²，因直径为d，故表面积为πd²，而正方体的表面积为6a²＝πd²，

∴d＞a，从而正方体的体积为a³＝d³·，

而V_球＝π³＝d³.

∵＜1，∴V_球＞V_正．

[答案]　A

5．已知三棱锥S-ABC的各顶点都在一个半径为r的球面上，球心O在AB上，SO⊥底面ABC，AC＝r，则球的体积与三棱锥体积之比是(　)

A．π　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．2π

C．3π　 　　　　　　　　　　　　　　　　　　　　　　　　 D．4π

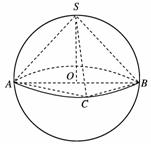
[解析]　∵SO⊥底面ABC，

∴SO为三棱锥的高线，

∴SO＝r，又∵O在AB上，AB＝2r，AC＝r，

∠ACB＝90°，∴BC＝r，

∴V_S-ABC＝××r×r×r＝r³.

又∵球的体积V＝πr³，

∴＝ ＝4π.

[答案]　D

4．(2008年湖南)长方体ABCD-A₁B₁C₁D₁的8个顶点在同一个球面上，且AB＝2，AD＝，AA₁＝1，则顶点A、B间的球面距离是(　)

A．2π　 　　　　　　　　　　　　　　　　　　　　　　 B.π

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　记长方体的外接球球心为O，半径为R，连结OA、OB，则有(2R)²＝2²+()²+1²＝8，R²＝2，OA²＝OB²＝2，在△AOB中，OA²+OB²＝AB²＝4，∠AOB＝.因此，顶点A、B间的球面距离等于×＝，选C.

[答案]　C

3．(2008年湖北)用与球心距离为1的平面去截球，所得的截面面积为π，则球的体积为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C．8π　 　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　S_圆＝πr²＝1⇒r＝1，而截面圆圆心与球心的距离d＝1，∴球的半径为R＝＝，

∴V＝πR³＝，故选B.

[答案]　B

2．(2008年江西)连结球面上两点的线段称为球的弦．半径为4的球的两条弦AB、CD的长度分别等于2、4，M、N分别为AB、CD的中点，每条弦的两端都在球面上运动，有下列四个命题：

①弦AB、CD可能相交于点M　②弦AB、CD可能相交于点N　③MN的最大值为5　④MN的最小值为1

其中真命题的个数为(　)

A．1个　 　　　　　　　　　　　　　　　　　　　　　　　 B．2个

C．3个　 　　　　　　　　　　　　　　　　　　　　　　　 D．4个

[解析]　当AB，CD相交时，是一个球的一个截面圆的两条弦，由AB＝<CD＝得，①是真命题，②是假命题；当以AB，CD为直径的两个小圆所在平面互相平行且在球心O的两侧时，MN最大，此时M，O，N三点共线，OM＝＝3，ON＝＝2，故MN的最大值为5；当以AB，CD为直径的两个小圆所在平面互相平行且在球心O的同侧时，MN最小，故MN的最小值为1，③，④是真命题，故选C.

[答案]　C

1．(2010年南充模拟)已知球面上的三个点A、B、C，且AB＝6，BC＝8，AC＝10，球半径R＝15，则球心到平面ABC的距离是(　)

A．10　 　　　　　　　　　　　　　　　　　　　　　　　　 B．10

C．15　 　　　　　　　　　　　　　　　　　　　　　　　　 D．15

[解析]　由题意截面圆的半径为5，

∴球心到截面距离d＝＝10.

[答案]　B

12．如图，已知平行六面体ABCD-A₁B₁C₁D₁的底面为正方形，O₁、O分别为上、下底面的中心，且A₁在底面ABCD内的射影为O.

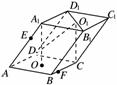
(1)求证：平面O₁DC⊥平面ABCD；

(2)若点E、F分别在棱AA₁、BC上，且AE＝2EA₁，问点F在何处时，EF⊥AD?

[解析]　(1)证明：如图，连结AC，BD，A₁C₁，则O为AC，BD的交点，O₁为A₁C₁，B₁D₁的交点．由平行六面体的性质知：A₁O₁∥OC，且A₁O₁＝OC，∴四边形A₁OCO₁为平行四边形，∴A₁O∥O₁C.

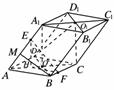
∵A₁O⊥平面ABCD，∴O₁C⊥平面ABCD.

又∵O₁C⊂平面O₁DC，∴平面O₁DC⊥平面ABCD.

(2)如图，作EH⊥平面ABCD，垂足为H，则EH∥A₁O，点H在直线AC上，且EF在平面ABCD内的射影为HF.

由三垂线定理及其逆定理知，若EF⊥AD，则HF∥AB.

∵AE＝2EA₁，∴AH＝2OH，从而CH＝2AH.

又∵HF∥AB，∴CF＝2BF，∴当F为BC的三等分点(靠近点B)时，有EF⊥AD.

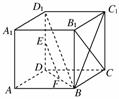
11．如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E、F分别为DD₁、DB的中点．

(1)求证：EF∥平面BC₁D₁；

(2)求证：EF⊥B₁C.

[证明]　(1)已知E、F分别为DD₁、DB的中点，EF是三角形BD₁D的中位线，

所以EF∥BD₁.

又EF⊄面BD₁C₁，BD₁⊂面BD₁C₁，

所以EF∥面BD₁C₁.

(2)正方体中D₁C₁⊥面BCC₁B₁，

B₁C⊂面BCC₁B₁，所以D₁C₁⊥B₁C.

在正方形BCC₁B₁中，两对角线互相垂直，

即BC₁⊥B₁C，又D₁C₁∩BC₁＝C₁，

所以B₁C⊥面BC₁D₁，又因为BD₁⊂面BC₁D₁，

所以B₁C⊥BD₁.

(1)中已证EF∥BD₁，所以EF⊥B₁C.

10．如图，在正三棱柱ABC-A₁B₁C₁中，AA₁＝AB＝a，F、F₁分别是AC、A₁C₁的中点．

(1)求证：平面AB₁F₁∥平面C₁BF；

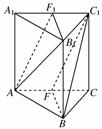(2)求证：平面AB₁F₁⊥平面ACC₁A₁.

[证明]　(1)在正三棱柱ABC-A₁B₁C₁中，

∵F、F₁分别是AC、A₁C₁的中点，

∴B₁F₁∥BF，AF₁∥FC₁.

又∵B₁F₁与AF₁是两相交直线，

BF与FC₁是两相交直线，

∴平面AB₁F₁∥平面C₁BF.

(2)在正三棱柱ABC-A₁B₁C₁中，

AA₁⊥平面A₁B₁C₁，

∴B₁F₁⊥AA₁.又B₁F₁⊥A₁C₁，A₁C₁∩AA₁＝A₁，

∴B₁F₁⊥平面ACC₁A₁，而B₁F₁⊂平面AB₁F₁，

∴平面AB₁F₁⊥平面ACC₁A₁.