3．若直线y＝kx+1与曲线x²+y²+kx－y＝0的两个交点恰好关于y轴对称，则k等于(　)

A．0　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．3

[解析]　由消去y得

(1+k²)x²+2kx＝0，

∴x₁＝0，x₂＝－.

∵两个交点关于y轴对称，

∴x₁＝－x₂，∴k＝0.

[答案]　A

2．设过点P(x，y)的直线分别与x轴的正半轴和y轴的正半轴交于A、B两点，点Q与点P关于y轴对称，O为坐标原点，若＝2，且·＝1，则P点的轨迹方程是(　)

A．3x²+y²＝1(x＞0，y＞0)

B．3x²－y²＝1(x＞0，y＞0)

C.x²－3y²＝1(x＞0，y＞0)

D.x²+3y²＝1(x＞0，y＞0)

[解析]　如图所示，若P(x，y)，则A，B(0,3y)，

＝，OQ(－x，y)，

∵·＝1，∴x²+3y²＝1(x＞0，y＞0)，

即为点P轨迹方程．

[答案]　D

1．方程|y|－1＝表示的曲线是(　)

A．抛物线　　　　　　　　　　　　　 B．一个圆

C．两个圆　 　　　　　　　　　　　　　　　　　　　　　 D．两个半圆

[解析]　原方程等价于

即或

[答案]　D

12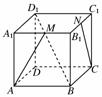．如图所示，正方体ABCD-A₁B₁C₁D₁中，M、N分别是A₁B₁、B₁C₁的中点．问：

(1)AM和CN是否是异面直线？说明理由．

(2)D₁B和CC₁是否是异面直线？说明理由．

[解析]　(1)不是异面直线．理由：

连接MN、A₁C₁、AC.

∵M、N分别是A₁B₁、B₁C₁的中点，

∴MN∥A₁C₁.

又∵A₁A綊C₁C，∴A₁ACC₁为平行四边形．

∴A₁C₁∥AC，得到MN∥AC，

∴A、M、N、C在同一平面内，故AM和CN不是异面直线．

(2)是异面直线．证明如下：

∵ABCD-A₁B₁C₁D₁是正方体，

∴B、C、C₁、D₁不共面，

假设D₁B与CC₁不是异面直线，

则存在平面α，使D₁B⊂平面α，CC₁⊂平面α，

∴D₁、B、C、C₁∈α，

∴与ABCD-A₁B₁C₁D₁是正方体矛盾．

∴假设不成立，即D₁B与CC₁是异面直线．

11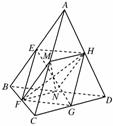．已知空间四边形ABCD的对角线AC、BD，点E、F、G、H、M、N分别是AB、BC、CD、DA、AC、BD的中点．求证：三线段EG、FH、MN交于一点且被该点平分．

[证明]　如图所示，连结EF、FG、GH、HE.

∵E、F、G、H分别为AB、BC、CD、DA的中点，

∴EF∥HG，EH∥FG，∴四边形EFGH是平行四边形．

设EG∩FH＝O，则O平分EG、FH.

同理，四边形MFNH是平行四边形，设MN∩FH＝O′，则O′平分MN、FH.

∵点O、O′都平分线段FH，

∴点O与点O′重合，

∴MN过EG和FH的交点，即三线段EG、FH、MN交于一点且被该点平分．

10．如图所示，在正方体ABCD-A₁B₁C₁D₁中，E为AB中点，F为AA₁中点，求证：E、C、D₁、F四点共面．

[证明]　分别连结EF、A₁B、D₁C，

∵E、F分别是AB和A₁A中点，

∴EF∥A₁B且EF=A₁B.

又∵A₁D₁綊B1C1綊BC，

∴四边形A₁D₁CB是平行四边形．

∴A₁B∥CD₁，从而EF∥CD₁.

由推论3，EF与CD₁确定一个平面．

∴E、F、C、D₁四点共面．

9．空间四边形ABCD中，各边长均为1，若BD＝1，则AC的取值范围是________．

[解析]　如图①所示，△ABD与△BCD均为边长为1的正三角形，当△ABD与△CBD重合时，AC＝0，将△ABD以BD为轴转动，到A，B，C，D四点再共面时，AC＝，如图②，故AC的取值范围是0<AC<.

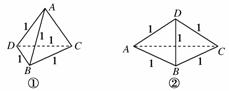
[答案]　(0，)

8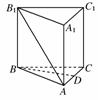．(2010年云南模拟)如图所示，在正三棱柱ABC－A₁B₁C₁中，D是AC的中点，AA₁∶AB＝∶1，则异面直线AB₁与BD所成的角为________．

[解析]　在平面ABC内，过A作DB的平行线AE，过B作BH⊥AE于H，

连接B₁H，则在Rt△AHB₁中，

∠B₁AH为AB₁与BD所成角，

设AB＝1，则A₁A＝，

∴B₁A＝，AH＝BD＝，

∴cos∠B₁AH＝＝，

∴∠B₁AH＝60°.

[答案]　60°

7．在图中，G、H、M、N分别是正三棱柱的顶点或所在棱的中点，则表示直线GH、MN是异面直线的图形有________．(填上所有正确答案的序号)

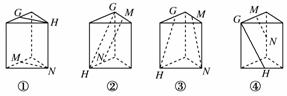
[解析]　如题干图①中，直线GH∥MN；

图②中，G、H、N三点共面，但M∉面GHN，因此直线GH与MN异面；

图③中，连接MG，GM∥HN，

因此GH与MN共面；

图④中，G、M、N共面，但H∉面GMN，

∴GH与MN异面．

所以图②、④中GH与MN异面．

[答案]　②、④

6．以下四个命题中，正确命题的个数是(　)

①不共面的四点中，其中任意三点不共线；

②若点A、B、C、D共面，点A、B、C、E共面，则A、B、C、D、E共面；

③若直线a、b共面，直线a、c共面，则直线b、c共面；

④依次首尾相接的四条线段必共面．

A．0　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．3

[解析]　①中若有三点共线，则四点共面，所以①正确；

②中，当A、B、C三点不共线时，正确；

当A、B、C三点共线时，A、B、C、D、E不一定共面；

③中，b、c可能共面，也可能异面；

④中以空间四边形为例知其错误．

综上，只有①正确．

[答案]　B