9．已知直线l：3x－y－1＝0，在l上求一点P，点P到点A(4,1)和B(0,4)的距离差最大，则P的坐标为________．

[解析]　先求点B关于直线3x－y－1＝0对称的点C的坐标(x，y)．

∴解得∴C(3,3)，

∴k_AC＝－2，

∴直线AC的方程为y－3＝－2(x－3)，即2x+y－9＝0，

直线AC与3x－y－1＝0的交点即为P点．

由解得P(2,5)．

[答案]　(2,5)

8．已知平面上一点M(5,0)，若直线上存在点P使|PM|＝4，则称该直线为“切割型直线”，下列直线中是“切割型直线”的是________(填上所有正确答案的序号)．

①y＝x+1；②y＝2；③y＝x；④y＝2x+1.

[解析]　本题考查点到直线的距离公式及对新定义的理解能力．根据题意，看所给直线上的点到定点M距离能否取4.可通过求各直线上的点到点M的最小距离，即点M到直线的距离来分析．①d＝＝3＞4，故直线上不存在点到点M距离等于4，不是“切割型直线”；②d＝2＜4，所以在直线上可以找到两个不同的点，使之到点M距离等于4，是“切割型直线”；③d＝＝4，直线上存在一点，使之到点M距离等于4，是“切割型直线”；④d＝＝＞4，故直线上不存在点到点M距离等于4，不是“切割型直线”．

[答案]　②③

7．两平行线l₁，l₂分别过点(1,0)与(0,5)，设l₁，l₂之间的距离为d，则d的取值范围是________．

[解析]　∵两点(1,0)与(0,5)的距离为，∴0＜d≤.

[答案]　(0，]

6．直线l过点(2,1)，且原点到l的距离是1，那么l的方程是(　)

A．x＝1或3x－4y+5＝0　 　　　　　　　　　　 B．y＝1或3x－4y－5＝0

C．y＝1或4x－3y－5＝0　 　　　　　　　　　　 D．x＝1或4x－3y－5＝0

[解析]　若l是x＝2，则原点到l的距离不等于1，设l的方程为y－1＝k(x－2)，

即kx－y－2k+1＝0，

∴＝1，解得k＝0或k＝，

∴l的方程为y－1＝0或y－1＝(x－2)

即y＝1或4x－3y－5＝0.

[答案]　C

5．设两条直线的方程分别为x+y+a＝0、x+y+b＝0，已知a、b是关于x的方程x²+x+c＝0的两个实数根，且0≤c≤，则这两条直线之间距离的最大值和最小值分别为(　)

A.，　 　　　　　　　　　　　　　　　　　　　　　　　 B.，

C.，　 　　　　　　　　　　　　　　　　　　　　　　　 D.，

[解析]　由题意a+b＝－1，ab＝c，

∴(a－b)²＝1－4c，∴≤(a－b)²≤1，

∴两平行线间距离d＝，

∴d²＝∈[，]，∴d∈[，]，

∴d的最大值为，最小值为.

[答案]　D

4．过点M(－2,4)作圆C：(x－2)²+(y－1)²＝25的切线l，又直线l₁：ax+3y+2a＝0与直线l平行，则直线l与l₁之间的距离是(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　由已知圆C的圆心C(2,1)，半径R＝5，

又点M在圆C上，k_MC＝－.

∴切线l的方程为y－4＝(x+2)，

即－4x+3y－20＝0.而l₁∥l，∴a＝－4，

∴l₁：－4x+3y－8＝0，

∴l与l₁间的距离d＝＝.

[答案]　B

3．三条直线l₁：x－y＝0，l₂：x+y－2＝0，l₃：5x－ky－15＝0构成一个三角形，则k的取值范围是(　)

A．k∈R

B．k∈R且k≠±1，k≠0

C．k∈R且k≠±5，k≠－10

D．k∈R且k≠±5，k≠1

[解析]　由l₁∥l₃得k＝5，由l₂∥l₃得k＝－5，

由得.若(1,1)在l₃上，则k＝－10.

故若l₁ ，l₂，l₃能构成一个三角形，

则k≠±5且k≠－10.

[答案]　C

2．(2008年金华模拟)若直线l₁、l₂在x轴上的截距都是a，在y轴上的截距都是b，则直线l₁与l₂(　)

A．平行　 　　　　　　　　　　　　　　　　　　　　　　　 B．重合

C．平行或重合　 　　　　　　　　　　　　　　　　　 D．相交或重合

[解析]　由题意，l₁，l₂都过点(a,0)，(0，b)，

若a＝b＝0，则l₁，l₂相交或重合．

若a≠b，则l₁，l₂重合．

[答案]　D

1．(2010年孝昌模拟)若动点A(x₁，y₁)，B(x₂，y₂)分别在直线l₁：x+y－7＝0和l₂：x+y－5＝0上移动，则线段AB的中点M到原点的距离的最小值为(　)

A．2　 　　　　　　　　　　　　　　　　　　　　　　　 B．3

C．3　 　　　　　　　　　　　　　　　　　　　　　　　 D．4

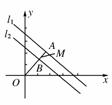
[解析]　由题知l₁∥l₂，过点O向l₁、l₂作垂线，垂足分别为A、B.

此时线段AB的中点M到原点的距离最小，原点到l₂的距离

d₁＝＝，

直线l₁、l₂间的距离为d₂＝＝，

∴|OM|＝+＝3.

[答案]　C

12．已知与曲线C：x²+y²－2x－2y+1＝0相切的直线l交x轴，y轴于A，B两点，且OA＝a，OB＝b(a＞2，b＞2)．

(1)求证：(a－2)(b－2)＝2；

(2)求线段AB的中点的轨迹方程；

(3)求△AOB面积的最小值．

[解析]　依题意直线l的方程为+＝1，

即bx+ay－ab＝0.

圆C的方程为(x－1)²+(y－1)²＝1.

(1)证明：∵直线l与圆C相切，

∴＝1，

化简得2－2a－2b+ab＝0，

即(a－2)(b－2)＝2.

(2)设AB的中点的坐标为(x，y)，

则a＝2x，b＝2y，

代入(1)式得(2x－2)(2y－2)＝2，

即(x－1)(y－1)＝.

(3)由(a－2)(b－2)＝2，得ab＝2a+2b－2.

S_△AOB＝ab＝a+b－1

＝(a－2)+(b－2)+3

≥2+3＝3+2，

当且仅当a＝b＝2+时，面积有最小值3+2.