
题目列表(包括答案和解析)
2.函数表达式的求法:①定义法;②换元法;③待定系数法.
1.相同函数的判定方法:①定义域相同;②对应法则相同(两点必须同时具备).
由于函数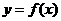 的零点就是方程
的零点就是方程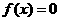 的根,所以在研究方程的有关问题,如:比较方程根的大小、确定方程根的分布、证明根的存在性等时,都可以将方程问题转化为函数问题,借助函数的零点,结合函数的图象加以解决.
的根,所以在研究方程的有关问题,如:比较方程根的大小、确定方程根的分布、证明根的存在性等时,都可以将方程问题转化为函数问题,借助函数的零点,结合函数的图象加以解决.
例2 已知函数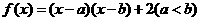 ,若
,若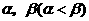 是方程
是方程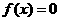 的两个根,则实数
的两个根,则实数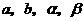 之间的大小关系是( )
之间的大小关系是( )
A.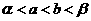 B.
B.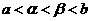
C.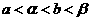 D.
D.
解析:若令 ,显然函数
,显然函数 的两个零点是
的两个零点是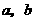 ,函数
,函数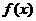 的两个零点是
的两个零点是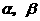 ,而函数
,而函数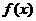 的图象是由函数
的图象是由函数 的图象向上平移两个单位得到的,结合图象可知:
的图象向上平移两个单位得到的,结合图象可知: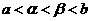 ,故应选(B).
,故应选(B).
例3
已知关于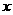 的方程
的方程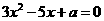 的两根
的两根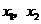 满足
满足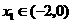 ,
,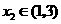 ,求实
,求实
数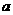 的取值范围.
的取值范围.
解析:依题意,关于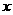 的方程
的方程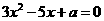 的两根
的两根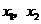 满足
满足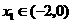 ,
,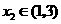 ,即函数
,即函数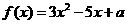 的两个零点
的两个零点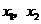 满足
满足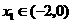 ,
,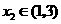 ,所以结合二次函数
,所以结合二次函数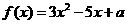 的图象可得:
的图象可得:
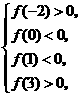 即
即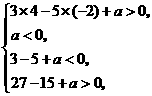 解得:
解得: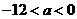 .
.
我们知道,二次函数的图象是连续的,当它通过零点(不是二重零点)时,函数值变号,
并且在任意两个相邻的变号零点之间函数值保持同号,根据二次函数变号零点的这一性质,可以求解二次不等式.
例1 二次函数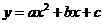 的部分对应值如下表:
的部分对应值如下表:
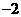
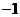

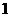
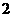
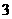
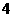
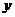
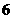

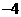
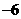
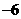
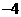

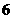
则不等式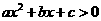 的解集是 .
的解集是 .
解析:由表中数据可知函数的两个零点分别为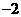 和
和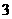 ,这两个零点将其余实数分为三个区间:
,这两个零点将其余实数分为三个区间: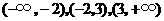 ,在区间
,在区间 )中取特殊值
)中取特殊值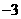 ,由于
,由于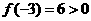 ,因此根据二次函数变号零点的性质可得:当
,因此根据二次函数变号零点的性质可得:当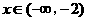 时,都有
时,都有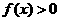 ;当
;当 时,有
时,有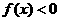 ;当
;当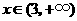 时,有
时,有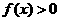 ,故不等式的解集为
,故不等式的解集为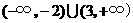 .
.
例3
已知函数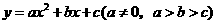 ,若
,若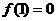 ,问:是否存在正整
,问:是否存在正整
数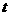 使
使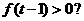 若存在,求出
若存在,求出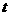 ;若不存在,请说明理由.
;若不存在,请说明理由.
解析:

至此可知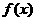 的开口向上,与
的开口向上,与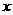 轴的两个交点一个是负数,另一个是1,由图象特征知
轴的两个交点一个是负数,另一个是1,由图象特征知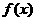 在
在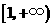 上是增函数,若
上是增函数,若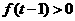 成立,由
成立,由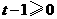 知,必有
知,必有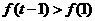 ,得
,得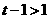 ,即
,即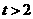 .
.
故正整数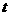 存在,且只要是大于
存在,且只要是大于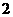 的正整数都满足
的正整数都满足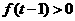 .
.
例2
一元二次方程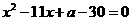 的两根都大于5,求实数
的两根都大于5,求实数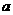 的范围.
的范围.
解析:按常规,设方程的两根分别为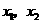 ,则
,则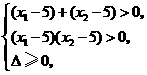
对于这个不等式组,求解的麻烦程度是可想而知的.
若我们设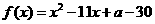 ,则其对称轴方程为
,则其对称轴方程为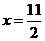 ,而函数的零点关于对称轴对称,因为欲使两根都大于5,只需限定较小的根大于5即可.
,而函数的零点关于对称轴对称,因为欲使两根都大于5,只需限定较小的根大于5即可.
由于开口向上,因此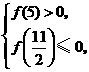
即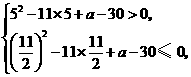 得
得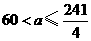 .
.
例1 若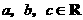 ,且
,且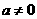 ,
,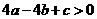 ,
, ,则下列结论正确的是( )
,则下列结论正确的是( )
A.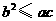
B.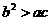
C.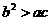 ,且
,且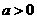
D.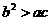 ,且
,且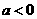
解析:结合已知,对照函数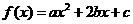 ,我们会发现
,我们会发现 ,
,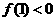 .这说明在
.这说明在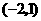 上函数存在一个零点,由于
上函数存在一个零点,由于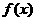 是二次函数,说明图象与
是二次函数,说明图象与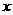 轴必有两个交点,也就是方程
轴必有两个交点,也就是方程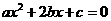 有两个不等的实根,因为
有两个不等的实根,因为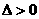 ,即
,即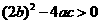 ,得
,得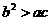 ,故答案为(B).
,故答案为(B).
12.已知△ABC的一个顶点A(-1,-4),内角∠B、∠C的角平分线所在直线方程分别是l1:y+1=0,l2:x+y+1=0,求BC边所在直线的方程.
[解析] 设点A(-1,-4)关于直线l1:y=-1的对称点E的坐标为(xE,yE),则xE=-1,yE=2(-1)-(-4)=2,
∴E(-1,2).
又设A(-1,-4)关于直线l2:x+y+1=0的对称点F的坐标为(xF,yF),则
⇒
∴F(3,0),由于E、F在BC上
且KEF==-
∴BC所在直线方程为y=-(x-3)
即x+2y-3=0
∴所求直线为3x+2y-7+(x-y+1)=0,
即5x-y-3=0.
11.已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
[解析] (1)∵l1⊥l2,
∴a(a-1)+(-b)·1=0,即a2-a-b=0①
又点(-3,-1)在l1上,
∴-3a+b+4=0②
由①②得a=2,b=2.
(2)∵l1∥l2,∴=1-a,∴b=,
故l1和l2的方程可分别表示为:
(a-1)x+y+=0,(a-1)x+y+=0,
又原点到l1与l2的距离相等.
∴4||=||,∴a=2或a=,
∴a=2,b=-2或a=,b=2.
10.求过直线l1:3x+2y-7=0与l2:x-y+1=0的交点,且平行于直线5x-y+3=0的直线方程.
[解析] 方法一:由,
得两直线交点为(1,2),
又5x-y+3=0的斜率为5,
∴所求直线为y-2=5(x-1), 即5x-y-3=0.
方法二:设所求直线方程为:
3x+2y-7+λ(x-y+1)=0,
即(λ+3)x+(2-λ)y-7+λ=0,
因此直线与5x-y+3=0平行,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com