

题目列表(包括答案和解析)
例3、某工厂转换机制,在两年内生产的月增长率都是a,则这两年内第二年某月的产
值比第一年相应月的增长率是多少?
错解:设第一年某月的产值为b,则第二年相应月的产值是 ,依题意所求增长率是
,依题意所求增长率是 ,或把第二年相应月的产值写成
,或把第二年相应月的产值写成
剖析:对增长率问题的公式 未透彻理解而造成错解的答案,或者是由于审题不慎密而造成题意的理解错误,若某月的产值是b,则此月第x个月后的产值是
未透彻理解而造成错解的答案,或者是由于审题不慎密而造成题意的理解错误,若某月的产值是b,则此月第x个月后的产值是
 ,指数x是基数所在时间后所跨过的时间隔数。
,指数x是基数所在时间后所跨过的时间隔数。
正解:不妨设第一年2月份的产值为b,则3月份的产值是b(1+a),4月份的产值是
 ,依此类推,到第二年2月份是第一年2月份后的第12个月,即一个时间间隔是一个月,而这里跨了12个月,故第二年2月份的产值是
,依此类推,到第二年2月份是第一年2月份后的第12个月,即一个时间间隔是一个月,而这里跨了12个月,故第二年2月份的产值是 ,又由增长率的概念知,这两年内的第二年某月的产值比第一年相应月的增长率为:
,又由增长率的概念知,这两年内的第二年某月的产值比第一年相应月的增长率为:
例2、某单位计划10月份组织员工到H地旅游,人数估计在10-25人之间。甲、乙两
旅行社的服务质量相同,且组织到H地的价格都是每人200元。该单位联系时,甲旅行社表示可给予每位游客七五折优惠;乙旅行社表示可免去一位游客的旅游费用,其余游客八折优惠,问该单位应该怎样选择,使其支付的旅游总费用较少?
错解:折该单位到H地旅游的人数为x,选择甲旅行社时,所需的费用为 元;选择乙旅行社时,所需的费用为
元;选择乙旅行社时,所需的费用为 元,则有:
元,则有: ,即
,即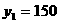 x;
x;
 ,即
,即
(1)若 ,解得x=16;
,解得x=16;
(2)若 ,解得
,解得 ;
;
(3)若 ,解得
,解得
所以,当人数为16人时选择甲旅行社或乙旅行社支付的总费用一样,即可任取一家;当人数在10-15人之间时,选取乙旅行社支付的总费用较少;当人数在17-25人之间时,选择甲旅行社,支付的总费用较少。
剖析:上述解法对10-19人时,解答虽然正确,但对于20-25人时,可将其划分为两组“享受免去两人的旅游费用”的特惠(分组后仍遵循每组10-25人条件,未犯原则,可行),则选择乙旅行社的支付的总费用较少。
正解:(1)当人数在10-15人或20-25人(分两组同游)时,选择乙旅行社;
(2)当人数在17-19人时,选择甲旅行社;
(3)当人数为16人时,任选甲、乙两旅行社之一都可。
例1 甲、乙两地相距S千米,汽车从甲地匀速行驶到乙地,速度不超过c千米/时.已知汽车每小时的运输成本(单位:元)由可变部分和固定部分组成:可变部分与速度V(千米/时)的平方成正比,比例系数为b;固定部分为a元,(I)把全程运输成本y(元)表示为速度V(千米/时)的函数,并指出这个函数的定义域;(II)为了使全程运输成本最小,汽车应以多大速度行驶?(已知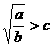 ).
).
分析:首先求出汽车从甲地到乙地所用的时间,然后建立全程运输成本的数学模型.
解:(I)依题意知汽车从甲地匀速行驶到乙地所用的时间为 ,全程运输成本为
,全程运输成本为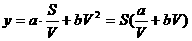
故所求函数及其定义域为: .
.
(II)当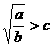 时,可以证明函数
时,可以证明函数 上是减函数,所以当
上是减函数,所以当 时,全程运输成本最小值是
时,全程运输成本最小值是 .
.
注:1.函数的单调性可用定义证明;2.本题若不给出已知条件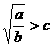 也可解,但要讨论.
也可解,但要讨论.
例2 公园要建造一个圆形的喷水池,在水池中央垂直于水面安装一个花形柱子OA.O恰好水面中心,OA=1.25(米)安置在柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路径落下,且在过OA的任一平面上抛物线路么如图所示,为使水流形状较漂亮,设计成水流到OA距离为1米处达到距水面最大高度2.25米,如果不计其它因素,那么池半径至少要多少米,才能使喷出的水流不致落到池外?
 分析:首先要建立适当的坐标系,写出抛物线的方程,求出水流落到水面上的点到点O的距离.
分析:首先要建立适当的坐标系,写出抛物线的方程,求出水流落到水面上的点到点O的距离.
解:如图建立平面直角坐标系,则设水流
所呈现的抛物的解析式可设为(顶点是(1,2.25)):

∵A(0,1.25),代入上式得,a=-1
于是抛物线为
令
∴水池半径至少要2.5米才能使水流不落到池外.
例3 在对口扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状况良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息货款没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,首先保证企业乙的全体职工每月最低生活费开支3600元后,逐步偿还转让费(不计息).在甲提供资料中有:①这种消费品的进价每件14元;②该店月销售量Q(百件)与销售价格P(元)的关系如图:③每月需支付各项开支2000元.
(1)试问为使该店至少能够维持职工生活,商品价格应控制在何范围内?
(2)当商品的价格为每件多少元时,月利润扣除职工最低生活费的余额最大?并求最大余额.
(3)企业乙只依靠该店,最早可望在几年后脱贫?
分析:本题应建立三个数学模型:①根据月销量图建立Q与P的函数关系;②建立利润余额函数;③建立脱贫不等式.

解:设该店月利润余额为L,则由题意得
L=Q(P-14)×100-3600-2000 ①
由销量图,得
Q= 
代入①式得:
L= 
(1)当14≤P≤20时,由L≥0得18≤P≤20,当20<P≤26时,由L≥0得20<P≤22.故商品销售价应控制在18≤P≤22的范围内.
(2)当14≤P≤20时,Lmax=1800(元),这时P=19.5元,当20<P≤22时,Lmax=1250(元),故当P=19.5元时,月利润余额最大,最大余额为1800元.
(3)设可在x年内脱贫,依题意有
12x×1800-50000-5800≥0
解得≥5.
即最早可望在5年后脱贫.
注:(2)中利用二次函数的图象来解
3. 根据已知条件建立函数关系式是函数应用的一个重要方面.这类问题有两类:一类根据几何、物理概念建立函数关系.另一类是通过观察、实验建立函数关系.例如自由落体的距离公式就属于观察实验建立的函数关系式.
2. 在解题中要充分运用数形结合、转化与化归、函数与方程等数学思想及策略,寻求解题途径.
1. 要解好数学应用问题,首先要增强应用数学的意识.一般来说,解决数学应用问题可分三步:第一步,理解题意,弄清关系;第二步,抓住关键、建立模型;第三步,数学解决、检验模型.其中第二步尤为关键.
能够运用函数的性质,特别是指数函数和对数函数的性质解决某些简单的实际问题,培养用数学的意识和分析问题、解决问题的能力.
注意幂函数、指数函数、对数函数模型的差异。在区间 上,尽管
上,尽管 都是增函数,但它们的增长速度不同,随着x的增长,
都是增函数,但它们的增长速度不同,随着x的增长, 的增长速度越来越快,会超过并远远超过
的增长速度越来越快,会超过并远远超过 的增长速度,而
的增长速度,而 的增长速度则会越来越慢,因此总会存在一个
的增长速度则会越来越慢,因此总会存在一个 ,当
,当 时就有
时就有 。
。
常用几类函数模型有一元一次、二次函数模型,分段函数模型,指数、对数函数模型以及幂函数模型和反比例函数模型等。
(1)一次函数及分段函数模型:
例1、铁路运输托运行李,从甲地到乙地,规定每张客票托运费计算方法为:行李质量不超过50kg,按0.25元/kg计算;超过50kg而不超过100kg时,其超过部分按0.35元/kg计算,超过100kg时,其超过部分按0.45元/kg计算。
(1) 计算出托运费用。
(2) 若行李质量为56kg,托运费用为多少?
分析:此题为分段函数,分段函数是一个函数,而不是几个函数,求分段函数的函数值时,应先确定自变量在定义域中的范围,然后按相应的对应法则求值。
解析:(1)设行李质量为xkg,托运费用为y元,则
①若 kg,则
kg,则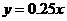 ;
;
②若50kg<x 100kg,则
100kg,则 ;
;
③若x>100kg,则 。
。
所以,由①②③可知

(2)因为50kg<56kg 100kg,所以
100kg,所以
点评:现实生活中很多事例可以用一次函数模型表示,如匀速直线运动的时间与位移的关系,弹簧的伸长与拉力的关系等,对一次函数来说,当一次项系数为正时,表现为匀速增长,即为增函数,一次项系数为负时为减函数。
(2)一元二次函数模型
例2、某商人将进货单价为8元的某种商品按10元一个销售时,每天可卖出100个。现在他采用提高售价,减少进货量的办法增加利润,已知这种商品销售单价每涨1元,销售量就减少10个,问他将售价每个定为多少元时,才能使每天所赚的利润最大?并求出最大值。
分析:①利润=销售总额-进货总额。
②基本关系,若设每个提价x元,利润为y元,应先弄清以下基本量:
日销量=(100-10x)个;
销售总额=(10+x)(100-10x)元;
进货总额=8(100-10x)元。这是解题的关键。
解析:设每个提价x元 ,利润为y元,每天销售总额为
,利润为y元,每天销售总额为 元;
元;
进货总额为 元,显然100-10x>0,x<10。
元,显然100-10x>0,x<10。

当 时,y取得最大值,此时销售单价为14元,最大利润为360元。
时,y取得最大值,此时销售单价为14元,最大利润为360元。
点评::利润问题是常见函数应用问题,通常要认清利润与价格以及销售量相互之间的制约关系,通过构造二次函数模型,利用二次函数求最值的方法解决相关的最值问题。借助二次函数模型求最值,是应用问题中的重要方法。
(3)指数、对数、幂函数模型
例3、某工厂今年1月、2月、3月生产某种产品分别为1万件、1.2万件、1.3件。为了估计以后每个月的产量,以这三个月的产品数量为依据,用一个函数来模拟该产品的月产量y与月份x的关系。模拟函数可以选择二次函数或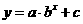 (其中a、b、c为常数),已知4月份该产品的产量为1.37万件,试问用以上哪个函数作为模拟函数较好?并说明理由。
(其中a、b、c为常数),已知4月份该产品的产量为1.37万件,试问用以上哪个函数作为模拟函数较好?并说明理由。
分析:比较两个模拟函数的优劣,就是比较月份与产量的关系反映得更准确,先根据前三个月份的数据用待定系数法求得解析式,在验证第四个月,比较误差即可。
解析:设两个函数 ,
, 。
。
依题意,有
所以 ,所以
,所以 (万件)。
(万件)。
依题意也有 ,所以
,所以
所以 。
。
经比较可知, 比
比 更接近于四月份的产量,所以选用
更接近于四月份的产量,所以选用 作模拟函数较好。
作模拟函数较好。
点评:本题为开放型的探究题,函数模型不确定,需要我们去探索,找到合适的模型,解题过程一般为:
(1)选择函数模型:一次函数为 ;二次函数为
;二次函数为 ;
;
幂函数型为 ;指数型函数为
;指数型函数为 。
。
(2)用待定系数法求出函数模型。
(3)检验:对求出的几个函数模型进行比较、验证,得出最合适的函数模型。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com