
题目列表(包括答案和解析)
1. 零点定理
如果函数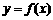 在区间
在区间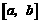 上的图象是连续不断的一条曲线,并且有
上的图象是连续不断的一条曲线,并且有
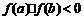 ,那么函数
,那么函数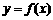 在区间
在区间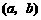 内有零点,即存在
内有零点,即存在 ,使得
,使得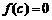 ,这个
,这个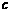 也就是方程
也就是方程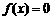 的根.
的根.
5.幂函数模型: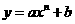 。
。
4.对数函数模型: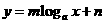 ;
;
3.指数函数模型: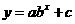 ;
;
2.二次函数模型: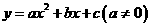 ;
;
1.一次函数模型: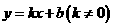 ;
;
3.解函数应用题的方法:一方面是利用已知函数模型解决问题,另一方面是建立恰当的函数模型,并利用所得函数模型解释有关现象。这一方法即是数学建模,这也是本节内容的一个难点.
2.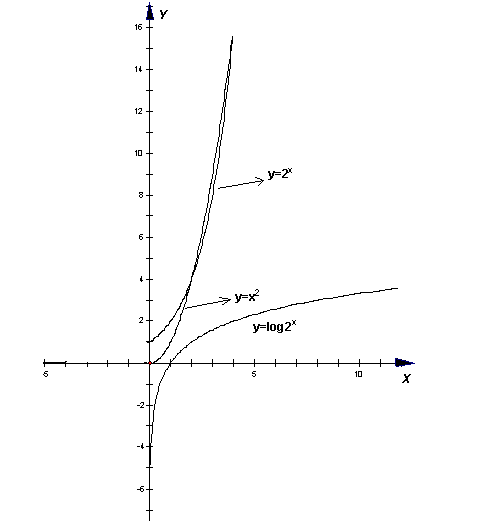 几类函数模型增长差异:在区间(0,+∞)上,尽管函数y=ax (a>1), y =㏒ax(a>1)和y=xn(n>0)都是增函数,但他们的增长速度不同,随着x的增大,y=ax (a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而且y = ㏒ax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x> x0时,就有㏒ax< xn< ax.
几类函数模型增长差异:在区间(0,+∞)上,尽管函数y=ax (a>1), y =㏒ax(a>1)和y=xn(n>0)都是增函数,但他们的增长速度不同,随着x的增大,y=ax (a>1)的增长速度越来越快,会超过并远远大于y=xn(n>0)的增长速度,而且y = ㏒ax(a>1)的增长速度则会越来越慢.因此,总会存在一个x0,当x> x0时,就有㏒ax< xn< ax.
注:以上结论要结合几个特殊函数(y=2x, y=㏒2x和y=x2)的图像进行理解:如图,刚开始函数y=㏒2x增长的最快,随后增长的速度越来越慢;而函数y=2x刚开始增长得较慢,随后增长的速度越来越快;函数y=x2增长的速度也是越来越快,但越来越不如y=2x增长得快,函数y=2x 和y=x2的图像有两个交点(2,4)和(4,16)。在x∈(2,4)时,㏒2x<2x< x2,在x∈(0,2)∪(2,4)时,㏒2x< x2<2x ,所以,当x>4时,总有㏒2x< x2<2x.
1.几类不同增长的函数模型:(1)一次函数模型:f(x)=kx+b (k,b为常数,k≠0);(2)反比例函数模型:f(x)=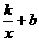 (k ,b为常数,k≠0);(3)二次函数模型:f(x)= ax2+bx+c(a,b,c为常数,a≠0);(4)指数函数模型:f(x)= abx+c(a,b,c为常数,a≠0,b>0,b≠1);(5)对数函数模型:f(x)=mlogax+n(m,n,a为常数,a>0,a≠1),(6)幂函数模型:f(x)=axn+b(m,n,b为常数,a≠0,n≠1).
(k ,b为常数,k≠0);(3)二次函数模型:f(x)= ax2+bx+c(a,b,c为常数,a≠0);(4)指数函数模型:f(x)= abx+c(a,b,c为常数,a≠0,b>0,b≠1);(5)对数函数模型:f(x)=mlogax+n(m,n,a为常数,a>0,a≠1),(6)幂函数模型:f(x)=axn+b(m,n,b为常数,a≠0,n≠1).
注:学习时应收集一些生活中普遍使用的函数模型(一次函数、二次函数、指数函数、对数函数、幂函数、分段函数等)的实例,了解函数模型的广泛应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com