
题目列表(包括答案和解析)
8.如图所示,在A,B间有四个焊接点,若焊接点脱落,则可能导致电路不通.今发现A、B之间线路不通,则焊接点脱落的不同情况有________种.
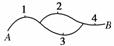
[解析] 本题考查分类和分步计数原理的应用.可采用排除法,各个焊点的情况各有2种情况,故四个焊点共有24种可能,其中能使线路通的情况是:1,4都通 ,2和3中至少有一个通时线路才通,共有3种可能,故不通的共有24-3=13种可能.
[答案] 13
7.(2010年珠海模拟)从5名外语系大学生中选派4名同学参加广州亚运会翻译、交通、礼仪三项义工活动,要求翻译有2人参加,交通和礼仪各有1人参加,则不同的选派方法共有________种.
[解析] 本题可分三步完成.
第一步:先从5人中选出2名翻译,共C种选法,
第二步:从剩余3人中选1名交通义工,共C种选法,
第三步:从剩余2人中选1名礼仪义工,共C种选法,
所以不同的选派方法共有CCC=60种.
[答案] 60
6.(2008年安徽高考题)12名同学合影,站成了前排4人后排8人.现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的种数是( )
A.CA B.CA
C.CA D.CA
[解析] 解决本题可分两个步骤:第一步:从后排8人中抽取2人,有C种方法;第二步:前排6人的排列,因为原来前排的4人顺序不变,所以有=A种方法(或者第二步是从前排的6个位置中选2个位置让抽出来的2人排好,剩余的4人按原顺序排好,有A种方法).根据分步乘法计数原理得共有CA种方法.
[答案] C
5.(2008年海南宁夏高考)甲、乙、丙3位志愿者安排在周一至周五的5天中参加某项志愿者活动,要求每人参加一天且每天至多安排一人,并要求甲安排在另外两位前面,不同的安排方法共有( )
A.20种 B.30种
C.40种 D.60种
[解析] 甲排周一时,有A=12种排法.
甲排周二时,有A=6种排法.
甲排周三时,有A=2种排法.
故共有12+6+2=20种不同的排法.
[答案] A
4.编号为1、2、3、4、5的5个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个人的编号与座位号一致的坐法有( )
A.10种 B.20种
C.30种 D.60种
[解析] 五个人有两个人的编号与座位号相同,此两人的选法共有C,假如编号1、2号人坐的号为1、2,其余三人的编号与座号不同,共有2种坐法.
∴符合题意的坐法为2×C=2×10=20种.
[答案] B
3.6个人分乘两辆不同的汽车,每辆车最多坐4人,则不同的乘法方法数为( )
A.40 B.50
C.60 D.70
[解析] 先分组再排列,一组2人一组4人有C=15种不同的分法;两组各3人共有=10种不同的分法,所以不同的乘法方法数为25×A=50.
[答案] B
2.将7名学生分配到甲、乙两个宿舍中,每个宿舍至少安排2名学生,那么互不相同的分配方案共有( )
A.252种 B.112种
C.70种 D.56种
[解析] 分两类:甲、乙每屋住4人、3人或5人、2人,所以共有CA+CA=35×2+21×2=112种.
[答案] B
1.在直角坐标系xOy平面上,平行直线x=m(m=0,1,2,3,4),与平行直线y=n(n=0,1,2,3,4)组成的图形中,矩形共有( )
A.25个 B.100个
C.36个 D.200个
[解析] 两条水平线与两条竖直线可组成一个矩形,所以矩形的个数也就是从5条水平线中取两条水平线,从五条竖直线中取两条竖直线的方法,所以共有C·C=100个.
[答案] B
2. 用二分法求函数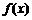 零点近似值的步骤(给定精确度为
零点近似值的步骤(给定精确度为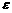 )
)
(1)
确定区间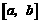 ,验证
,验证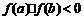 ,给定精确度
,给定精确度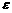 ;
;
(2)
求区间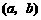 的中点
的中点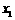 ;
;
(3)
计算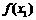 ;
;
①
若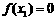 ,则
,则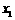 就是函数的零点;
就是函数的零点;
②
若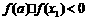 ,则令
,则令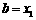 ,(此时零点
,(此时零点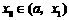 );
);
③
若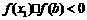 ,则令
,则令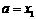 ,(此时零点
,(此时零点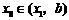 );
);
(4)
判断是否达到精确度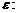 即若
即若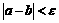 ,则得到零点近似值
,则得到零点近似值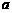 (或
(或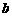 );否则重复(2)-(4).
);否则重复(2)-(4).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com