2．(2008年广东高考)设a∈R，若函数y＝e^x+ax，x∈R有大于零的极值点，则(　)

A．a＜－1　 　　　　　　　　　　　　　　　　　　　　　 B．a＞－1

C．a＞－　 　　　　　　　　　　　　　　　　　　　　　 D．a＜－

[解析]　∵y＝e^x+ax，∴y′＝e^x+a.

又∵函数y＝e^x+ax有大于零的极值点，即方程y′＝e^x+a＝0有大于零的解，即a＝－e^x(x＞0)．

∵x＞0时，－e^x＜－1，∴a＜－1.

[答案]　A

1．函数f(x)的定义域为开区间(a，b)，导函数f′(x)在(a，b)内的图象如图所示，则函数f(x)在开区间(a，b)内有极小值点的个数为(　)

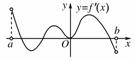
A．1　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．2

C．3　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．4

[解析]从f′(x)的图象可知f(x)在(a，b)内从左到右的单调性依次为增?减?增?减，∴在(a，b)内只有一个极小值点．

[答案]　A

12．现有高三四个班学生34人，其中一、二、三、四班各7人、8人、9人、10人，他们自愿组成数学课外小组．

(1)选其中一人为负责人，有多少种不同的选法？

(2)每班选一名组长，有多少种不同的选法？

(3)推选二人发言，这二人需来自不同的班级，有多少种不同的选法？

[解析]　(1)分四类，第一类，从一班学生中选1人，有7种选法；第二类，从二班学生中选1人，有8种选法；第三类，从三班学生中选1人，有9种选法；第四类，从四班学生中选1人，有10种选法，所以，共有不同的选法N＝7+8+9+10＝34种．

(2)分四步，第一、二、三、四步分别从一、二、三、四班学生中选一人任组长，所以共有不同的选法

N＝7×8×9×10＝5 040种．

(3)分六类，每类又分两步，从一、二班学生中各选1人，有7×8种不同的选法；从一、三班学生中各选1人，有7×9种不同的选法；从一、四班学生中各选1人，有7×10种不同的选法；从二、三班学生中各选1人，有8×9种不同的选法；从二、四班学生中各选1人，有8×10种不同的选法；从三、四班学生中各选1人，有9×10种不同的选法，

所以共有不同的选法N＝7×8+7×9+7×10+8×9+8×10+9×10＝431种．

11．在7名学生中，有3名会下象棋但不会下围棋，有2名会下围棋但不会下象棋，另2名既会下象棋又会下围棋．现在从会下象棋和会下围棋的学生中各选1人同时分别参加象棋比赛和围棋比赛，共有多少种不同的选法？

[解析]　选参加象棋比赛的学生有两种选法：在只会下象棋的人中选或在既会下象棋又会下围棋的人中选；选参加围棋比赛的学生也是同样的道理．由此可得不同的选法有：CC+CC+CC+A＝18种，

故不同的选法有18种．

10．2008年9月27日16时34分，神舟七号宇航员翟志刚出舱进行太空行走，17时00分35秒返回．某校全体师生集体观看了电视实况转播，观看后组织全体学生进行关于“太空行走”的论文评选．若高一年级共4个班，每班评出两篇优秀论文(男、女生各一篇)，把这些优秀论文平均分成四组进行展览，且每组都有男、女生所写论文，则不同的展览方式共多少种？

[解析]　论文分四组展览，可分四步完成：

第一步：先选第一组，因为每组男、女生都有，

所以共4×4＝16种选法；

第二步：选第二组，共3×3＝9种选法；

第三步：选第三组，共2×2＝4种选法；

第四步：确定第四组，共1×1＝1种选法．

由分步乘法计数原理知，不同的展览方式共有：

16×9×4×1＝576种．

9．某校开设9门课程供学生选修，其中A、B、C三门由于上课时间相同，至多选一门，学校规定，每位同学选修4门，共有________种不同的选修方案．(用数值作答)

[解析]　第一类，若从A、B、C三门选一门有C·C＝60种，

第二类，若从其他六门中选4门有C＝15种，

∴共有60+15＝75种不同的方法．

[答案]　75

8．(2008年浙江高考)用1,2,3,4,5,6组成六位数(没有重复数字)，要求任何相邻两个数字的奇偶性不同，且1和2相邻，这样的六位数的个数是________．(用数字作答)

[解析]　

若1在①或⑥号位，2在②或⑤号位，方法数各4种．

若1在②、③、④、⑤号位，2的排法有2种，方法数各8种，

故有4+4+8+8+8+8＝40个．

[答案]　40

7．一排共9个座位，甲、乙、丙三人按如下方式入座：每人左右两旁都有空座位，且甲必须在乙、丙两人之间，则不同的坐法共有________种(用数字作答)．

[解析]　从左到右9个位子中，甲只能坐4、5、6三个位子．当甲位于第5个位子时，乙、丙只能在2、3或7、8中的一个位子上；当甲位于第4个位子时，乙、丙肯定有一个位于2，另一个位于6、7、8中的一个位子上；当甲位于第6个位子时，乙、丙肯定有一个位于8，另一个位于2、3、4中的一个位子上，故共有4×2+3×2+3×2＝20种．

[答案]　20

6．将正方体ABCD-A₁B₁C₁D₁的各面涂色，任何相邻两个面不同色，现有5种不同颜色，并且涂好了过A点的三个面的颜色，那么其余3个面的涂色方案共有(　)

A．13种　 　　　　　　　　　　　　　　　　　　　 B．14种

C．12种　 　　　　　　　　　　　　　　　　　　　 D．11种

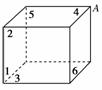
[解析]　将正方体六个面分别标为1,2,3,4,5,6.

不妨假设4,5,6面已涂好，如图，再涂1,2,3面．

(1)1面与6面颜色相同．若3面与5面相同，2面有3种涂法，若3面与5面不同，3面有2种涂法，此时2面也有2种涂法，

∴共有3+2×2＝7种．

(2)1面与6面颜色不同．

1面有2种涂法，若3面与5面相同，2面有2种涂法，若3面与5面不同，2面只有1种涂法，

∴共有2×(2+1)＝6种．

由分类加法计数原理，共有7+6＝13种涂法．

[答案]　A

5．(2008年湖北)将5名志愿者分配到3个不同的奥运场馆参加接待工作，每个场馆至少分配一名志愿者的方案种数为(　)

A．540　 　　　　　　　　　　　　　　　　　　　　 B．300

C．180　 　　　　　　　　　　　　　　　　　　　　　 D．150

[解析]　要将5名志愿者分配到3个不同的地方，每个地方至少一人，首先要将这5个人分成3组，因此有2种分组方案：1,1,3与1,2,2.

当按1,1,3方案分组时，有C·A＝60种方法；

当按1,2,2方案分组时，先进行平均分组，有＝15种分组方法，

因此有15×A＝90种方法．所以一共有60+90＝150种分法，故选D.

[答案]　D