10．已知函数f(x)＝x³－3x及y＝f(x)上一点P(1，－2)，过点P作直线l.

(1)求使直线l和y＝f(x)相切且以P为切点的直线方程；

(2)求使直线l和y＝f(x)相切且切点异于P的直线方程．

[解析]　(1)由f(x)＝x³－3x得，f′(x)＝3x²－3，

过点P且以P(1，－2)为切点的直线的斜率f′(1)＝0，

∴所求直线方程为y＝－2；

(2)设过P(1，－2)的直线l与y＝f(x)切于另一点(x₀，y₀)，

则f′(x₀)＝3x－3.

又直线过(x₀，y₀)，P(1，－2)，

故其斜率可表示为＝，

又＝3x－3，

即x－3x₀+2＝3(x－1)·(x₀－1)，

解得x₀＝1(舍)或x₀＝－，

故所求直线的斜率为k＝3×(－1)＝－，

∴y－(－2)＝－(x－1)，即9x+4y－1＝0.

9．已知f(x)，g(x)都是定义在R上的函数，g(x)≠0，f′(x)g(x)＜f(x)g′(x)，f(x)＝a^x·g(x)，+＝，在有穷数列{}(n＝1,2，…，10)中，任意取前k项相加，则前k项和大于的概率是________．

[解析]　据已知得[]′＝＜0，

故a^x＝为定义域上的减函数，

故0＜a＜1，从而由+＝⇒a＝，

故易知数列{}即{a_n}从第五项开始其和大于，

故其概率为＝.

[答案]　

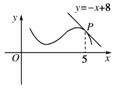
8．如图，函数y＝f(x)的图象在点P处的切线方程是y＝－x+8，则f(5)+f′(5)＝______.

[解析]　易得切点P(5,3)，

∴f(5)＝3，k＝－1，

即f′(5)＝－1.

∴f(5)+f′(5)＝3－1＝2.

[答案]　2

7．(2008年江苏高考)设直线y＝x+b是曲线y＝lnx(x＞0)的一条切线，则实数b的值为______．

[解析]　y′＝(lnx)′＝，令＝得x＝2，

∴切点为(2，ln2)，代入直线方程y＝x+b，

∴ln2＝×2+b，∴b＝ln2－1.

[答案]　ln2－1

6．(2008年辽宁高考)设P为曲线C：y＝x²+2x+3上的点，且曲线C在点P处切线倾斜角的取值范围为，则点P横坐标的取值范围为(　)

A.　　　　　　　　　　　　　　　 B．[－1,0]

C．[0,1]　 　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　设P(x₀，y₀)，∵y′＝2x+2，

∴曲线C在P点处的切线斜率为2x₀+2.

又切线倾斜角范围是[0，]，∴斜率范围是[0,1]，

即0≤2x₀+2≤1，∴－1≤x₀≤－.

[答案]　A

5．(2010年临沂模拟)若点P是曲线y＝x²－lnx上任意一点，则点P到直线y＝x－2的最小距离为(　)

A．1　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　过点P作y＝x－2的平行直线，且与曲线

y＝x²－lnx相切，

设P(x₀，x－lnx₀)则有

k＝y′|x＝x₀＝2x₀－.

∴2x₀－＝1，∴x₀＝1或x₀＝－(舍去)．

∴P(1,1)，

∴d＝＝.

[答案]　B

4．曲线y＝e^x在点(2，e²)处的切线与坐标轴所围三角形的面积为(　)

A.e²　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．2e²

C．e²　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　∵点(2，e²)在曲线上，

∴切线的斜率k＝y′_x＝2＝e²，

∴切线的方程为y－e²＝e²(x－2)．

即e²x－y－e²＝0.

与两坐标轴的交点坐标为(0，－e²)，(1,0)，

∴S_△＝×1×e²＝.

[答案]　D

3．已知二次函数f(x)的图象如图所示，则其导函数f′(x)的图象大致形状是(　)

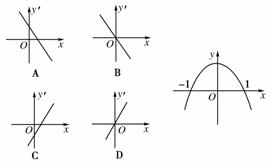
[解析]　设二次函数为y＝ax²+b(a＜0，b＞0)，则y′＝2ax，又∵a＜0，故选B.

[答案]　B

2．一质点沿直线运动，如果由始点经过t秒后的位移为s＝t³－t²+2t，那么速度为零的时刻是(　)

A．0秒　 　　　　　　　　　　　　　　　　　　　　　　　　　　 B．1秒末

C．2秒末　 　　　　　　　　　　　　　　　　　　　　　　　　 D．1秒末和2秒末

[解析]　∵s＝t³－t²+2t，

∴υ＝s′(t)＝t²－3t+2，

令υ＝0得，t²－3t+2＝0，t₁＝1，t₂＝2.

[答案]　D

1．设正弦函数y＝sin x在x＝0和x＝附近的平均变化率为k₁，k₂，则k₁，k₂的大小关系为 (　)

A．k₁＞k₂　 　　　　　　　　　　　　　　　　　　　　　　　　　 B．k₁＜k₂

C．k₁＝k₂　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．不确定

[解析]　∵y＝sin x，∴y′＝(sin x)′＝cos x，

k₁＝cos 0＝1，k₂＝cos ＝0，∴k₁＞k₂.

[答案]　A