1．设随机变量ξ-B，则P(ξ＝3)的值为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　 D.

[解析]　由已知P(ξ＝3)＝C³³＝.

[答案]　A

12．下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据．

(1)请画出上表数据的散点图；

(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程＝bx+a；

(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？(参考数值：3×2.5+4×3+5×4+6×4.5＝66.5)

[解析]　(1)由题设所给数据，可得散点图如下

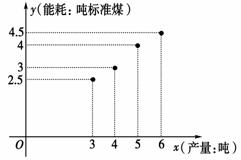
(2)由对照数据，计算得＝86，＝＝4.5，

＝＝3.5，

已知_iy_i＝66.5，所以线性回归方程的系数为：

b＝＝＝0.7，

a＝－b＝3.5－0.7×4.5＝0.35.

因此，所求的线性回归方程为＝0.7x+0.35.

(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗，能降低的生产能耗为：90－(0.7×100+0.35)＝19.65(吨标准煤)．

11．某中学

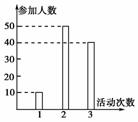
号召学生在今年春节期间至少参加一次社会公益活动(以下简称活动)．该校合唱团共有100名学生，他们参加活动的次数统计如图所示．

(1)求合唱团学生参加活动的人均次数；

(2)从合唱团中任选两名学生，求他们参加活动次数恰好相等的概率；

(3)从合唱团中任选两名学生，用ξ表示这两人参加活动次数之差的绝对值，求随机变量ξ的分布列及数学期望Eξ.

[解析]　由图可知，参加活动1次、2次和3次的学生人数分别为10、50和40.

(1)该合唱团学生参加活动的人均次数为

＝＝2.3.

(2)从合唱团中任选两名学生，他们参加活动次数恰好相等的概率为

P₀＝＝.

(3)从合唱团中任选两名学生，记“这两人中一人参加1次活动，另一人参加2次活动”为事件A，“这两人中一人参加2次活动，另一人参加3次活动”为事件B，“这两人中一人参加1次活动，另一人参加3次活动”为事件C.易知

P(ξ＝1)＝P(A)+P(B)＝+＝；

P(ξ＝2)＝P(C)＝＝；

又P(ξ＝0)＝P₀＝.

ξ的分布列：

ξ的数学期望：Eξ＝0×+1×+2×＝.

10．某煤矿有采煤工人400人，运输工人302人，管理和服务人员250人．要从中抽取190人组成职工代表参加讨论奖金分配方案，试确定用何种方法抽取，三种类型的职工各抽多少？

[解析]　由于奖金分配涉及到各种人的利益不同，所以应采用分层抽样方法．

因为总体人数400+302+250＝952(人)，

＝5余2，应剔除2人，

而＝80(人)，＝60(人)，＝50(人)，

所以，采煤工人、运输工人、管理和服务人员分别抽取80人、60人、50人．

9．(2008年广东)为了调查某厂工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量．产品数量的分组区间为[45,55)，[55,65)，[65,75)，[75,85)，[85,95)，由此得到频率分布直方图如图，则这20名工人中一天生产该产品数量在[55,75)的人数是________．

[解析]　由[55,75)的频率为0.04×10+0.025×10＝0.65，

得0.65×20＝13.

[答案]　13

8．为考虑广告费用x与销售额y之间的关系，抽取了5家餐厅，得到如下数据：

现要使销售额达到6万元，则需广告费用为________．(保留两位有效数字)

[解析]　先求出回归方程y＝bx+a，令y＝6，得x＝1.5万元．

[答案]　1.5万元

7．在某项测量中，测量结果ξ服从正态分布N(1，σ²)(σ＞0)，若ξ在(0,1)内取值的概率为0.4，则ξ在(0,2)内取值的概率为________．

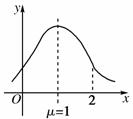
[解析]　依题意，如图，正态分布曲线的对称轴为μ＝1，又ξ在(0,1)内取值的概率为0.4，根据对称性ξ在(0,2)内取值的概率为0.8.

[答案]　0.8

0.03+0.05+0.05+0.07)×2＝0.4，

∴100名学生中体重在[56.5,64.5)的学生总数为100×0.4＝40(人)．

[答案]　C

6．为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5-18岁的男生体重(kg)，得到频率分布直方图如图所示：

根据如图所示可得这100名学生中体重在[56.5,64.5)的学生人数是(　)

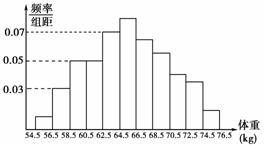
A．20　 　　　　　　　　　　　　　　　　　　　　　 B．30

C．40　 　　　　　　　　　　　　　　　　　　　　　 D．50

[解析]　根据落在各区间内的样本频率等于对应小矩形的面积求解．

体重在[56.5,64.5)的矩形面积之和为

5．如果随机变量ξ-N(μ，σ²)，且Eξ＝3，Dξ＝1，则P(－1<ξ≤1)等于(　)

A．2Φ(1)－1　 　　　　　　　　　　　　　　　　 B．Φ(4)－Φ(2)

C．Φ(2)－Φ(4)　 　　　　　　　　　　　　　　 D．Φ(－4)－Φ(－2)

[解析]　对正态分布，μ＝Eξ＝3，σ²＝Dξ＝1，故

P(－1<ξ≤1)＝Φ(1－3)－Φ(－1－3)

＝Φ(－2)－Φ(－4)＝Φ(4)－Φ(2)．

[答案]　B