
题目列表(包括答案和解析)
例3函数f(x)定义在正整数集上,且满足:f(1)=2002和f(1)+f(2)+……+f(n)=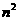 f(n),则f(2002)的值为__________.
f(n),则f(2002)的值为__________.
[分析]首先根据所给的条件求出f(n)的表达式,在求值.
[解析]由f(1)+f(2)+…+f(n)=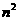 f(n),得:f(1)+f(2)+…+f(n-1)=
f(n),得:f(1)+f(2)+…+f(n-1)= f(n-1),两式相减得:f(n)=
f(n-1),两式相减得:f(n)=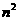 f(n)-
f(n)- f(n-1)(n≥3),变形得:
f(n-1)(n≥3),变形得: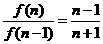 (n≥3),由
(n≥3),由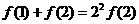 得:
得: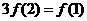 ,又f(1)=2002,于是有
,又f(1)=2002,于是有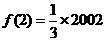 ,∴
,∴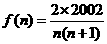 ,故f(2002)=
,故f(2002)=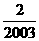 .
.
[点评]由f(n)=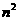 f(n)-
f(n)- f(n-1)(n≥3)推出f(n)的表达式,整个运算过程,都需要有一定的观察分析能力,善于从式子结构出发,向下进行,进而求出f(2002).
f(n-1)(n≥3)推出f(n)的表达式,整个运算过程,都需要有一定的观察分析能力,善于从式子结构出发,向下进行,进而求出f(2002).
例4已知函数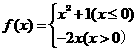 ,若f(x)=10,求x=_________.
,若f(x)=10,求x=_________.
[分析]首先确定用那一部分的函数表达式求解x,从f(x)=10可以看出,要求函数的值是正数,故不用f(x)=-2x(x>0).
[解析]由于f(x)=10>0,而当f(x)=-2x(x>0)时,f(x)<0,于是应用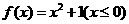 ,令
,令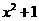 =10,x=±3,由于x<0,故x=-3.
=10,x=±3,由于x<0,故x=-3.
例1 已知y=f(x)满足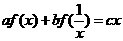 ,其中a、b、c都是非零的常数,a≠±b,求函数的解析式.
,其中a、b、c都是非零的常数,a≠±b,求函数的解析式.
[分析]y=f(x)没有具体结构,条件中的a、b、c a、b、c都是已知的常数,不可用待定系数法去求解.本题可用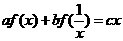 ,转化出另一个式子,采用解方程组的办法求解.
,转化出另一个式子,采用解方程组的办法求解.
[解析]∵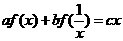 ,以
,以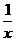 代换x得:
代换x得: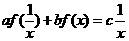 ,联立两式消去f(
,联立两式消去f(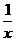 )得:
)得: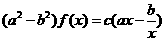 .∵
.∵ ,∴
,∴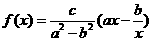 .
.
[点评]从所给式子出发,看成一个变式,把x换成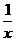 以后得到方程组,故视f(x)为一个未知量,解之得f(x),称此法为“函数方程法”.求抽象函数解析式这是常用的方法.
以后得到方程组,故视f(x)为一个未知量,解之得f(x),称此法为“函数方程法”.求抽象函数解析式这是常用的方法.
例2 设f(x)是定义域为R的函数,且满足f(-x)=-f(x),当x∈[0,+∞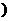 时,
时,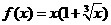 ,求f(x)的解析式.
,求f(x)的解析式.
[分析]利用f(-x)=-f(x)求(-∞,0)上的表达式即可.
[解析]∵f(-x)=-f(x),又当x<0时,-x>0,由已知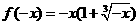 ,∴
,∴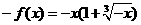 ,则
,则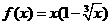 (x<0
(x<0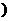 ,
,
∴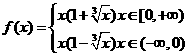 .
.
[点评]给出某区间上的表达式,求对称区间上的表达式时,常常应用f(-x)=-f(x)或f(-x)= f(x)进行转化.
4.构建指数函数模型解决实际问题
例4 某城市现有人口总数为100万人,如果年自然增长率为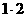 ℅,试解答下面的问题:(1)写出该城市人口总数
℅,试解答下面的问题:(1)写出该城市人口总数 (万人)与年份
(万人)与年份 (年)的函数关系式;
(年)的函数关系式;
(2)计算大约多少年以后该城市人口将达到120万人(精确到1年).
分析:本题属于人口增长率问题,第(2)小题要取常用对数计算.
解:(1)1年后该城市人口总数为:
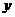 =100+100×
=100+100×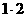 ℅=100(1+
℅=100(1+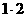 ℅)
℅)
2年后该城市人口总数为:
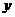 =100(1+
=100(1+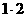 ℅)+100(1+
℅)+100(1+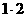 ℅)×
℅)×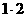 ℅=100
℅=100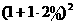
3年后该城市人口总数为:
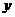 =100
=100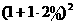 +100
+100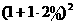 ×
×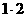 ℅=100
℅=100
… …
 年后该城市人口总数为:
年后该城市人口总数为: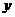 =100
=100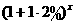
(2)设 年后该城市人口将达到120万人,即100
年后该城市人口将达到120万人,即100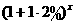 =120
=120
∴ 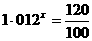 ,两边取常用对数得:
,两边取常用对数得: =
=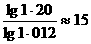 (年)
(年)
答:大约15年以后该城市人口将达到120万人.
3.构建分段函数模型解决实际问题
例3.“依法纳税是每个公民应尽的义务”,国家征收个人工资、薪金所得税是分段计算的:总收入不超过1000元的,免征个人工资薪金所得税;超过1000元的部分需征税.设全月纳税所得额(所得额指工资,薪金中应纳税的部分)为 ,
, =全月收入-1000元,税率见下表:
=全月收入-1000元,税率见下表:
 级数 全月纳税所得额
级数 全月纳税所得额 税率
税率
1 不超过500元部分 5℅
2 超过500元至2000元部分 10℅
3 超过2000元至5000元部分 15℅
9 超过100000部分 45℅
(1)若应纳税额为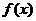 ,试用分段函数表示1-3级纳税额
,试用分段函数表示1-3级纳税额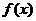 的计算公式;
的计算公式;
(2)某人2004年10月份工资总收入为4200元,试计算这个人10月份应纳个人所得税多少元?
分析:本题是分段累进计算问题.应注意分清段,计算清楚.
(1)
依税率表得:第一段: ·5℅
·5℅
第二段:( -500)×10℅+500×5℅
-500)×10℅+500×5℅
第三段:( -2000)×15℅+1500×10℅+500×5℅
-2000)×15℅+1500×10℅+500×5℅
即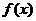 =
=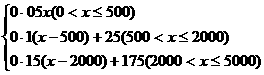
(2)这个人10月份个人所得税为: =4200-1000=3200,
=4200-1000=3200,
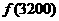 =
=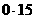 (3200-2000)+175=355(元)
(3200-2000)+175=355(元)
答:这个人10月份应缴纳个人所得税355元.
2.构建二次函数模型解决实际问题
例2 某商人如果将进货单价为8元的商品按每件10元售出时,每天可销售100件,现在它采用提高销售价,减少进货量的办法增加利润.已知这种商品每涨1元,其销售数就减少10个.问他将售出价定为多少,才能使赚得利润最大?
分析:利润=销售总额-进货总额
解:设每件提价 元(
元( ≥0),利润为
≥0),利润为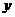 元.每天销售额为(10+
元.每天销售额为(10+ )(100-10
)(100-10 )元,进货总额为8(100-10
)元,进货总额为8(100-10 ).显然,100-10
).显然,100-10 >0,
>0, <10.
<10.
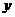 =(10+
=(10+ )(100-10
)(100-10 )-8(100-10
)-8(100-10 )(0≤
)(0≤ <10)
<10)
 =(2+
=(2+ )(100-10
)(100-10 )=-10
)=-10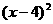 +360
+360
当 =4时,
=4时,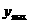 =360元.
=360元.
故当售出价为每件14元时,每天所赚得的利润最大为360元.
说明:画出函数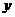 =-10
=-10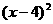 +360 (0≤
+360 (0≤ <10)的图形,从图象可以看出,当提价超过4元时,利润下降,当利润下降时商人就要考虑经营的方法,不应只考虑提价,而要降价,薄利多销.
<10)的图形,从图象可以看出,当提价超过4元时,利润下降,当利润下降时商人就要考虑经营的方法,不应只考虑提价,而要降价,薄利多销.
1.构建一次函数模型解决实际问题
例1 某厂在甲、乙两地的两个分厂生产某种机器12台和6台,现销售给A地10台,B地8台,已知从甲地调运一台到A地、B地的费用分别是400元和800元,从乙地调运一台至A地、B地的费用分别是300元和500元.
(1)
设从乙地要调运 台至A地,求总费用
台至A地,求总费用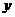 关于
关于 的函数关系式;
的函数关系式;
(2) 求若使总费用不超过9000元,问共有几种调运方案?
(3) 求出总费用最低的调运方案及最低的费用.
解:(1)因从乙地调运 台到A地,那么需从甲地调运(10-
台到A地,那么需从甲地调运(10- )台至A地;由题意,从乙地调往B地为(6-
)台至A地;由题意,从乙地调往B地为(6- )台,则从甲地调往B地应为[12-(10-
)台,则从甲地调往B地应为[12-(10- )]台,即(2+
)]台,即(2+ )台.从而有
)台.从而有
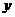 =300
=300 +500(6-
+500(6- )+400(10-
)+400(10- )+800(2+
)+800(2+ )
)
=200( +43) (0≤
+43) (0≤ ≤6,且
≤6,且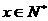 )
)
(2)当0≤ ≤2时,
≤2时,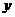 ≤9000,故共有3种调运方案,总费用不超过9000元.
≤9000,故共有3种调运方案,总费用不超过9000元.
(3)在(1)中,当 =0时,费用最低,调运方案是:乙地6台全部调往B地,甲地调2台至B地,10台运往A地,使总费用最低为
=0时,费用最低,调运方案是:乙地6台全部调往B地,甲地调2台至B地,10台运往A地,使总费用最低为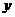 =8600元.
=8600元.
3.常见的函数模型
(1)一次函数模型: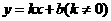 ;
;
(2)二次函数模型: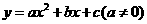 ;
;
(3)指数函数模型: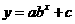 ;
;
(4)对数函数模型: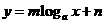 ;
;
(5)幂函数模型:
2.解决应用问题的基本步骤
(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择模型;
(2)建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
(3)求模:求解数学模型,得出数学结论;
(4)还原:将利用数学知识和方法得出的结论,还原为实际问题的意义。
此四步用框图可表示为:
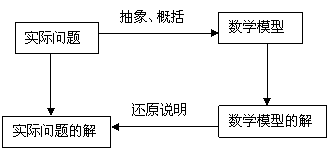
不同的函数模型能够刻画现实世界不同的变化规律,函数模型可以处理生产、生活中很多实际问题,因此学习中应注意:
1.根据实际应用问题的条件建立函数模型,并运用函数的概念和性质来解决实际问题,这类问题的建模方法有两种:一是根据几何和物理概念建立函数关系式;另一种是通过观察和实验建立函数关系式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com