
题目列表(包括答案和解析)
当关于某些抽象函数的命题不易从正面直接证明时,可采用反证法,它往往需结合其它一些求解策略,而此法是处理“是否存在”型函数综合题的常用方法.
例5 已知函数f(x)在区间(﹣∞,+∞)上是增函数,a、b∈R,(1)求证:若a+b≥0,则f(a)+f(b)≥f(﹣a)+f(﹣b);(2)判断(1)中命题的逆命题是否正确,并证明你的结论.
证明:(1)由a+b≥0,得a≥﹣b,
由函数f(x)在区间(﹣∞,+∞)上是增函数,得f(a)≥f(﹣b),同理,f(b)≥f(﹣a),
∴f(a)+f(b)≥f(﹣b)+f(﹣a),即f(a)+f(b)≥f(﹣a)+f(﹣b).
(2)中命题的逆命题是:若f(a)+f(b)≥f(﹣a)+f(﹣b),则a+b≥0,此逆命题为真命题,
现用反证法证明如下:
假设a+b≥0不成立,则a+b<0,a<﹣b,b<﹣a,
根据单调性,得f(a)<f(﹣b),f(b)<f(﹣a),f(a)+f(b)<f(﹣a)+f(﹣b),
这与已知f(a)+f(b)≥f(﹣a)+f(﹣b)相矛盾,故a+b<0不成立,
即a+b≥0成立,因此(1)中命题的逆命题是真命题.
根据题目所给的条件,分析、探求函数具有哪些特殊的性质,比如:函数的单调性、奇偶性、周期性、对称性等等,然后充分利用这些性质进行求解.
例3 f(x)是定义在R上的函数,且满足如下两个条件:①对于任意x,y∈R,有f(x+y)=f(x)+f(y);②当x>0时,f(x)<0,且f(1)=﹣2.求函数f(x)在[﹣3,3]上的最大值和最小值.
分析:设0≤x1≤x2≤3,由条件①得f(x2)=f[(x2﹣x1)+x1]=f(x2﹣x1)+f(x1),即f(x2﹣x1)=f(x2)﹣f(x1),
∵x2﹣x1>0,由条件②得f(x2﹣x1)<0,∵f(x2)﹣f(x1)<0,即f(x2)<f(x1),∴f(x)在[0,3]上是减函数,
在条件①中令x=y=0,则f(0+0)=f(0.)+f(0),∴f(0)=0.
再令x=﹣y,得f(x﹣x)=f(x)+f(﹣x),∴f(﹣x)=﹣f(x),∴f(x)是奇函数,
∴f(x)在[﹣3,0]上是减函数,
又∵当x<0时f(x)=﹣f(﹣x)>0,从而f(x)在[﹣3,3]上是减函数,
∴f(x)max=f(﹣3)=﹣f(3)=﹣f(1+2)=﹣f(1)﹣f(2)=﹣f(1)﹣f(1)﹣f(1)=﹣3f(1)=6,
f(x)min=f(3)=﹣f(﹣3)=﹣6.
例4 已知函数f(x)=ax5+bsinx+3,且f(﹣3)=7,求f(3)的值.
解析:f(x)的解析式中含有两个参数a、b,却只有一个条件f(﹣3)=7,无法确定出a、b的值,因此函数f(x)(解析式不确定)是抽象函数,注意到g(x)=ax5+bsinx=f(x)﹣3是奇函数,可得g(﹣3)=﹣g(3),即f(﹣3)﹣3=﹣[f(3)﹣3],f(3)=6﹣f(﹣3)=﹣1.
根据题设条件中所给等式或不等式的结构特点及欲证的结论,将题中的某些量替换为的需要的量(要注意新换的变量的取值范围,要与原题设条件等价),可以得到较为简单的等式或不等式,然后再设法作进一步的转化从中获解,
例2 已知函数f(x)存在反函数且f(x)+f(﹣x)=2,则f-1(x﹣1)+f-1(3﹣x)=________.
分析:本题无法直接求出f-1(x),若将已知等式左边看成两个函数,利用变量代换,则有如下简解:
令y1=f(x),y2=f(﹣x),则x=f-1(y1),﹣x=f-1(y2),且当y1+y2=2时,有f-1(y1)+f-1(y2)=x﹣x=0,
∵(x﹣1)+(3﹣x)=2,∴f-1(x﹣1)+f-1(3﹣x)=0.
赋值主要从以下方面考虑:①令x=…,﹣2,﹣1,0,1,2,…等特殊值求抽象函数的函数值;②令x=x2,y=x1或y=,且x1<x2,判定抽象函数的单调性;③令y=﹣x,判定抽象函数的奇偶性;④换x为x+T,确定抽象函数的周期;⑤用x=+或换x为等来解答有关抽象函数的其它一些问题.
例1 已知函数的定义域为R,对任意x、y满足f(x+y)=f(x)+f(y),当x>0时,f(x)>0.试判断f(x)的奇偶性和单调性.
分析:在f(x+y)=f(x)+f(y)中,令x=y=0,得f(0)+f(0)=0,∴f(0)=0,
又令y=﹣x,f(x)+f(﹣x)=f(x﹣x)=f(0)=0,即f(﹣x)=﹣f(x),∴f(x)是奇函数,
再设x1、x2∈R,且x1<x2,且在f(x+y)=f(x)+f(y)中,令x=x2,y=﹣x1,则f(x2﹣x1)=f(x2)+f(﹣x1)
由f(x)是奇函数得,f(x2)﹣f(x1)=f(x2)+f(-x1)=f(x2﹣x1),
∵x2﹣x1>0,∴f(x2﹣x1)>0,从而f(x2)>f(x1),∴f(x)在(﹣∞.+∞)上是增函数.
例12 设函数是定义在R上的增函数,且f(x)≠0,对于任意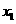 、
、 都有
都有 .
.
(1) 求证:f(x)>0;
(2) 求证: ;
;
(3)若f(1)=2,解不等式f(3x) >4f(x).
[分析]由于函数 具有本例中f(x)的条件与结构,因而在求解过程中应以指数函数
具有本例中f(x)的条件与结构,因而在求解过程中应以指数函数 (a>0且a≠1)为模型类比求解.
(a>0且a≠1)为模型类比求解.
[解析](1)令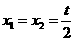 ,则
,则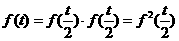 ,∵f(t) ≠0,
,∵f(t) ≠0,
∴f(t) >0,即f(x) >0,.
(2)∵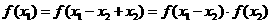 ,又f(x) ≠0,
,又f(x) ≠0,
∴ .
.
(3)∵f(1)=2,∴2f(x)= f(1) ·f(x)= f(1+x),4 f(x)=2·2 f(x)= f(1)·f(1+x)= f(2+x),∴f(3x) >4f(x),即f(3x) >f(2+x).又f(x)是定义域R上的增函数,∴3x>2+x,∴x>1,故不等式f(3x) >4f(x)的解集为{x|x>1}.
[点评]在解有关抽象函数问题时,可以根据题中的抽象函数关系式的特例,即具体函数,类比求解,这样可以使解题方向明确.
例13 已知函数f(x)的定义域为(0,+∞)且在其上为增函数,满足f(xy)=f(x)+f(y),f(2)=1,试解不等式f(x)+f(x-2)<3.
[分析]解此题的关键是求函数值3所对应的自变量值,即求f(a)=3中a的值.
[解析]∵f(4)=f(2)+f(2)=2,又3=2+1= f(4)+f(2)= f(4×2)= f(8),即f(8)=3,根据题中关系式,有f(x)+ f(x-2)=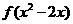 ,所以,原不等式化成
,所以,原不等式化成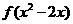 < f(8),有
< f(8),有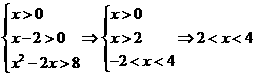 ,∴不等式的解集为{x|2≤x≤4}.
,∴不等式的解集为{x|2≤x≤4}.
例11 已知定义域为 的函数f(x),对任意x、y∈
的函数f(x),对任意x、y∈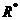 恒有f(xy)=f(x)+f(y).
恒有f(xy)=f(x)+f(y).
(1)求证:当x∈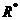 时,
时, ;
;
(2)若x>1时,恒有 ,求证:f(x)必有反函数;
,求证:f(x)必有反函数;
(3)设 是f(x)的反函数,求证:
是f(x)的反函数,求证: 在其定义域内恒有
在其定义域内恒有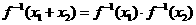 .
.
证明:(1)∵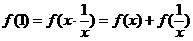 ,则有f(1)= f(1)+f(1) ,∴有f(1)=0,∴
,则有f(1)= f(1)+f(1) ,∴有f(1)=0,∴ .
.
(2)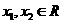 ,且
,且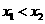 时,
时, ,∴
,∴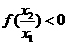 .
.
由 ,得
,得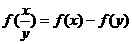 ,
,
∴ ,知f(x)在
,知f(x)在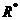 上为单调递减函数.∴f(x)必有反函数.
上为单调递减函数.∴f(x)必有反函数.
(3)设 ,∴
,∴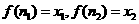 ,
, ,即
,即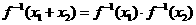 .
.
例12
已知函数 ,其定义域为
,其定义域为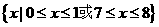 .
.
(1)若f(x)在其定义域内有反函数,求t的取值范围;
(2)在(1)的条件下,求反函数 .
.
解:(1)∵f(x)在 时其对称轴为x=t.
时其对称轴为x=t.
当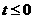 时,f(x)在其定义域内为增函数,所以此时f(x)有反函数;
时,f(x)在其定义域内为增函数,所以此时f(x)有反函数;
同理,当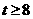 时,f(x)在其定义域内也有反函数;
时,f(x)在其定义域内也有反函数;
当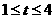 时,f(x)图象在
时,f(x)图象在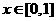 的一段比在
的一段比在 的一段更靠近对称轴.那么要使得f(x)在定义域内有反函数,应有
的一段更靠近对称轴.那么要使得f(x)在定义域内有反函数,应有 .
.
则得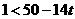 ,解得
,解得 ;
;
当 时,同理应有
时,同理应有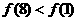 ,解得
,解得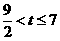 ;
;
当 时f(x)显然不存在反函数.
时f(x)显然不存在反函数.
有以上讨论可知,f(x)在其定义域内有反函数的t的范围为: .
.
(2)由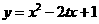 ,得
,得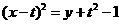 .
.
当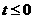 时知,
时知,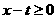 ,∴
,∴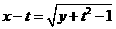 .
.
∴此时反函数为 ,其中
,其中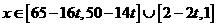
当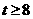 时,
时,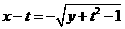 .
.
∴此时反函数为 ,其中
,其中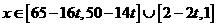
当 时,反函数为
时,反函数为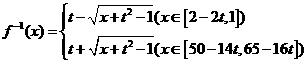 .
.
3、周期性
例10设f(x) 定义在R上的偶函数,其图象关于直线x=1对称,对任意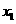 、
、
 都有
都有 ,且f(1)=a>0.
,且f(1)=a>0.
(1)求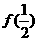 、
、 ;
;
(2)证明f(x)是周期函数.
[分析]偶函数的图象关于y轴对称,由函数图象关于直线x=1对称,可以判定函数f(x)是周期函数.
[解析](1)由 ,
,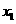 、
、
 ,知
,知 ,x∈[0,1],∵
,x∈[0,1],∵ ,
, ,又f(1)=a>0,∴
,又f(1)=a>0,∴ ,
,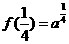 .
.
(2)依题意设y=f(x)关于直线x=1对称,∴f(x)= f(1+1-x),f(x)= f(2-x),又∵f(-x) =f(x),∴f(x)= f(x+2),∴函数f(x)是R上的周期函数,且2是它的一个周期.
2、奇偶性
例9 设f(x)是定义在R上的函数,满足f(x+2)=-f(x),且x∈[0,2]时,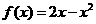 .
.
(1)求x∈[-2,0]时,f(x)的表达式;
(2)求f(9)和f(-9)的值;
(3)证明f(x)是奇函数.
[分析]这是一个分段函数问题,首先求出函数的表达式,然后在利用定义证明函数是奇函数.
[解析](1)∵x∈[-2,0]时,x+2∈[0,2],∴f(x)=-f(x+2)=-[2(x+2)-(x+2)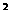 ],即x∈[-2,0]时,
],即x∈[-2,0]时, .
.
(2)∵f(x+2)=-f(x),∴f(x+4)=-f(x+2)= f(x),∴f(x)是以4为周期的周期函数.∴f(9)=f(1)=1,f(-9)= f(-1)=-1,.
(3)∵ ,
,
又∵f(x)+f(-x)= ,∴f(x)+f(-x)=0,(x∈[-2,2]),∴f(x)在[-2,2]上为奇函数.若x∈[4k-2,4k+2],k∈Z,则-x∈[-4k-2, -4k +2],,∴f(x)=
f(x-4k),f(-x)= f(-x+4k),且x-4k与-x+4k∈[-2,2]又∵-x+4k=-(x-4k),∴f(-x+4k)=-f(x-4k), ∴f(-x)=-f(x),∴f(x)为奇函数.
,∴f(x)+f(-x)=0,(x∈[-2,2]),∴f(x)在[-2,2]上为奇函数.若x∈[4k-2,4k+2],k∈Z,则-x∈[-4k-2, -4k +2],,∴f(x)=
f(x-4k),f(-x)= f(-x+4k),且x-4k与-x+4k∈[-2,2]又∵-x+4k=-(x-4k),∴f(-x+4k)=-f(x-4k), ∴f(-x)=-f(x),∴f(x)为奇函数.
1、单调性
例7 已知函数y=f(x)的定义域为R,对任意x∈R,均有f(x+x)=f(x)+f(x),且对任意x>0,都有f(x)<0,f(3)=-3.
(1)证明函数y=f(x)是R上的单调减函数;
(2)试求函数y=f(x)在[m,n](m,n∈Z且mn<0=上的值域.
[分析]利用函数的单调性的定义证明;由(1)的结论可知f(m)、f(n)分别是函数y=f(x)在[m,n]上的最大值与最小值,故求出f(m)与f(n)即可得所求函数的值域.
[证明](1)任取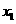 、
、 ,且
,且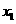 <
< ,
, ,由题设f(x+x)=f(x)+f(x),可知
,由题设f(x+x)=f(x)+f(x),可知 ,∵
,∵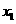 <
< ,∴
,∴ -
-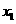 >0,∴f(
>0,∴f( -
-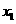 )<0, ∴
)<0, ∴ <
<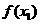 ,故y=f(x)是R上的单调减函数.
,故y=f(x)是R上的单调减函数.
(2)由于y=f(x)是R上的单调减函数,∴y=f(x)在[m,n]上也是单调递减函数,∴y=f(x)的最大值为f(m),最小值为f(n),∵f(n)=f[1+(n-1)]=f(1)+f(n-1)=2f(1)+f(n-2)=……=nf(1),同理f(m)= m f(1).
∵f(3)=-3,∴f(3)=3 f(1) =-3,∴f(1)=-1,f(m)=-m,f(n)=-n,故函数y=f(x)在[m,n]上的值域为[-n ,-m].
[点评]:对于抽象函数,往往通过研究函数的单调性确定其最值和值域;对抽象函数关系式中的变元取适当的值,求所需关系式或值,是解决抽象函数问题的常用技巧.
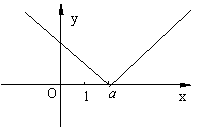 例8 若函数f(x)=|x-a|在(-∞,1)内是减函数,求实数a的取值范围.
例8 若函数f(x)=|x-a|在(-∞,1)内是减函数,求实数a的取值范围.
[分析]本题采用数形结合的方法形象直观容易求a的取值范围.
[解析]f(x)=|x-a|= ,作出函数的图象,由于(-∞,a)内是减函数,而在(-∞,1)内也是减函数,故(-∞,1)是(-∞,a)的子区间.
,作出函数的图象,由于(-∞,a)内是减函数,而在(-∞,1)内也是减函数,故(-∞,1)是(-∞,a)的子区间.
因此a≥1.
例5 已知函数y=f(2x+1)的定义域是[0,1],求y=f(x)的定义域.
[分析]函数y=f(2x+1)的定义域是[0,1],是指解析式中x的取值范围,2x+1不是自变量,而是中间变量,f(2x+1)中的中间变量相当于f(x)中的x,所以此题是已知x∈[0,1],求2x+1的取值范围.
[解析]∵函数y=f(2x+1)的定义域是[0,1],∴0≤x≤1,∴1≤2x≤3,∴函数y=f(x)的定义域是[1,3].
[点评]若已知函数y=f(x)的定义域为[a,b],求y=f(g(x))的定义域,只需将g(x)代换为x,解不等式a≤g(x)≤b,,求出x的集合即为y=f(g(x))的定义域;若已知y=f(g(x))的定义域为[a,b],求函数y=f(x)的定义域,只要求出y= g(x) ,x∈[a,b],的值域即为y=f(x)的定义域.
例6 已知函数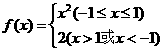 ,求其定义域和值域.
,求其定义域和值域.
[分析]求分段函数的定义域只要将各段的子区间取并集;求分段函数的值域需要分段求出值域,在取并集.
 [解析],由于[-1,1]∪(1,+∞)∪(-∞,-1)=R,可知,定义域为R.
[解析],由于[-1,1]∪(1,+∞)∪(-∞,-1)=R,可知,定义域为R.
当x∈[-1,1]时,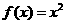 ,f(x) ∈[0,1];而当x∈(1,+∞)∪(-∞,-1)时,f(x)=2,因此函数
,f(x) ∈[0,1];而当x∈(1,+∞)∪(-∞,-1)时,f(x)=2,因此函数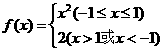 的值域为:[0,1] ∪{2}.
的值域为:[0,1] ∪{2}.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com