
题目列表(包括答案和解析)
2.已知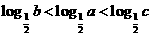 ,则( )
,则( )
 .
.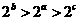
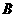 .
.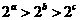
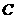 .
.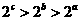
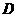 .
.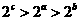
1.下列大小关系正确的是( )
 .
.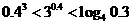
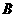 .
.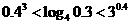
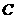 .
.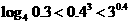
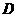 .
.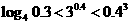
5.对数函数是许多知识的交汇点,是历年高考的必考内容,在高考中主要考查:定义域、值域、图象、对数方程、对数不等式、对数函数的主要性质(单调性等)及这些知识的综合运用,同时也常与其他知识相综合,出现难度较大的解答题。
例1 已知函数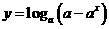 ,求它的定义域和值域,其中
,求它的定义域和值域,其中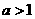 。
。
解析:(1)∵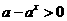 ,∴
,∴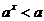 ,
,
又∵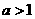 ,∴
,∴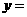
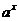 是增函数,∴
是增函数,∴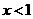 。
。
(2)∵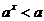 ,且
,且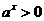 ,∴
,∴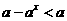 ,∴
,∴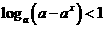 。
。
故函数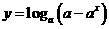 的定义域和值域分别为
的定义域和值域分别为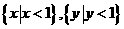 。
。
评注:求函数的定义域、值域问题是一个复杂的问题,求定义域时,要把限制条件摆全,勿要遗漏,对数函数真数的允许值范围要记熟,求函数值域时,千万不要忘记函数的定义域。
例2 求证函数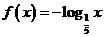 在
在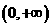 上是增函数。
上是增函数。
证明:在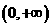 上任取两点
上任取两点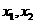 ,且
,且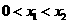 ,则
,则
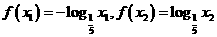
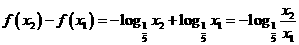
∵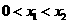 ,∴
,∴ ,而
,而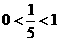 ,∴
,∴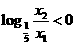 ,
,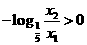 。
。
即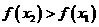 ,∴
,∴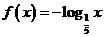 在
在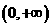 上是增函数。
上是增函数。
评注:该例是用函数单调性的定义解答的,这种方法是解决函数单调性最基本、最重要的方法。
例3 若实数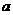 满足
满足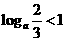 ,求
,求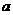 的取值范围。
的取值范围。
当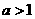 时,∵
时,∵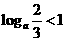 ,又
,又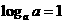 ,∴
,∴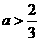 。
。
当 时,∵
时,∵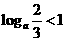 ,又
,又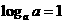 ,∴
,∴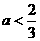 ,即
,即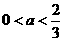 。
。
故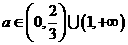 。
。
评注:解含有对数符号的不等式时,必须注意对数的底数是大于1还是小于1,然后再利用相应的对数函数的单调性进行解答。
练习:
4.解题过程中要注意灵活运用数形结合思想、分类讨论思想、等价转化思想等数学方法。
3.比较指数函数与对数函数类型的数值间的大小关系问题是高考中常见题型,具体解法是:(1)底数相同指数不同时,要考虑指数函数的单调性;(2)底、指数都不同时要借助中间值(如0或1);(3)比较两个对数的大小,关键是构造对数函数,若底数不相同时,可运用换底公式化为同底数的对数,同时还要注意与0比较或与1比较;再不行可考虑商值(或差值)比较法。
2.对数函数与指数函数互为反函数,要注意它们的图象、性质之间的区别和联系。
1.解答有关对数问题时,一要注意对数函数的定义域,二要注意底数的取值范围。
即通过对图像(或表格)中的数量关系进行分析来建立问题数学模型的方法。
例3某医药研究所开发一种新药,如果成人按规定的剂量使用,据监测,服药后每毫升血液中的含药量y与时间t之间近似满足如图曲线
(1)写出服药后y与t之间的函数关系式;
(2)据测定,每毫升血液中含药量不少于4微克时治疗疾病有效,假若某病人一天中第一次服药为7:00,问一天中怎样安排服药时间、次数,效果最佳?
[解] (1)依题意,得y=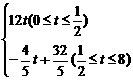
(2)设第二次服药时,在第一次服药后t1小时
则-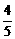 t1+
t1+ =4,t1=3
=4,t1=3
因而第二次服药应在10:00
设第三次服药在第一次服药后t2小时,则此时血液中含药量应为两次服药后含药量之和,即有-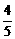 t2+
t2+ -
-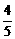 (t2-3)+
(t2-3)+ =4
=4
解得:t2=7(小时)
设第四次服药在第一次服药后t3小时(t3>8),则此时第一次服的药已吸收完,此时血液中含药量应为第二、三次之和
-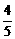 (t3-3)+
(t3-3)+ +[-
+[-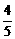 (t3-7)+
(t3-7)+ ]=4
]=4
解得t3=10.5小时
故第四次服药应在17:30.
例4 20个劳动力种50亩地,这些地可种蔬菜、棉花、水稻.这些作物每亩地所需劳力和预计产值如下表.应怎样计划才能使每亩地都能种上作物(水稻必种),所有劳力都有工作且作物预计总产值达最高?
|
作物 |
劳力/备 |
产值/亩 |
|
蔬菜 |
1/2 |
0.6万元 |
|
棉花 |
1/3 |
0.5万元 |
|
水稻 |
1/4 |
0.3万元 |
分析:题中显示“产值最高”的语句,应从构造有关产值的函数关系入手.
解:设种 亩水稻(
亩水稻(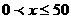 ),
),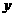 亩棉花(
亩棉花(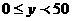 )时,总产值为
)时,总产值为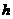 且每个劳力都有工作.
且每个劳力都有工作.
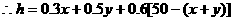 且
且 、
、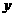 满足
满足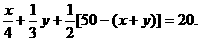
即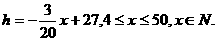
欲使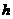 为最大,则
为最大,则 应为最小,故当
应为最小,故当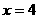 (亩)时,
(亩)时,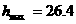 万元,此时
万元,此时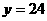 (亩).
(亩).
故安排1人种4亩水稻,8人种24亩棉花,11人种22亩蔬菜时农作物总产值最高且每个劳力都有工作.
即通过列表的方式探索问题的数学模型的方法。
例3 某工厂在甲、乙两地的两个分厂各生产某种机器12台和6台.现销售给A地10台,B地8台.已知从甲地调运1台至A地、B地的运费分别为400元和800元,从乙地调运1台至A地、B地的运费分别为300元和500元.
(1)设从乙地调运x台至A地,求总运费y关于x的函数关系式;
(2)若总运费不超过9000元,问共有几种调运方案;
(3)求出总运费最低的调运方案及最低的运费.
分析 由甲、乙两地调运至A、B两地的机器台数及运费如下表:
|
调出地 |
甲 地 |
乙 地 |
||
|
调至地 |
A地 |
B地 |
A地 |
B地 |
|
台数 |
10-x |
12-(10-x) |
x |
6-x |
|
每台运费(元) |
400 |
800 |
300 |
500 |
|
运费合计(元) |
400(10-x) |
800[12-(10-x)] |
300x |
500(6-x) |
解:(1)依题意,得
y=400(10-x)+800[12-(10-x)]+300x+500(6-x),
即y=200(x+43)(0≤x≤6,x∈Z).
(2)由y≤9000,解得x≤2.
∵x∈Z,0≤x≤6,∴x=0,1,2.
所以共有三种调运方案.
(3)由一次函数的单调性知,当x=0时,总运费y最低,
ymin=8600(元).
即从乙地调6台给B地,甲地调10台给A地、调2台给B地的调运方案的总运费最低,最低运费为8600元.
说明 本题数量关系较多,利用列表法将数量关系明朗化,有利于函数关系的准确建立.
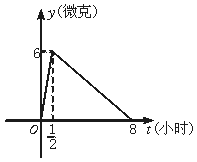
即通过寻找关键词和关键量之间的数量关系的方法来建立问题的数学模型的方法。
例1 进货原价为80元的商品400个,按90元一个售出时,可全部卖出.已知这种商品每个涨价一元,其销售数就减少20个,问售价应为多少时所获得利润最大?
分析:题中显示“利润最大”的语句,应从构造有关利润的函数关系入手.(利润=售额-成本)
解:设售价为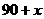 元时利润为
元时利润为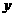 ,此时售量为
,此时售量为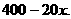
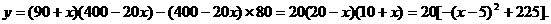 当
当 时,
时,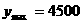 (元).
(元).
答:售价为95元时获利最大,其最大值为4500元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com