
题目列表(包括答案和解析)
2.当两根中有且仅有一根在区间(α,β)内,方程系数所满足的充要条件:
∵α<x1<β或α<x2<β,对应的函数f(x)的图象有下列四种情形(图2)

从四种情形得充要条件是:
f(α)·f(β)<0 ②
1.当两根都在区间(α,β)内,方程系数所满足的充要条件:
∵α<x1<x2<β,对应的二次函数f (x)的图象有下列两种情形(图1)
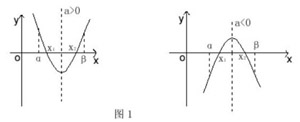
当a>0时的充要条件是:Δ>0,α<-b/2a<β,f(α)>0,f (β)>0
当a<0时的充要条件是:Δ>0,α<-b/2a<β,f(α)<0,f (β)<0
两种情形合并后的充要条件是:
Δ>0,α<-b/2a<β,af(α)>0,af (β)>0 ①
2、利用函数零点研究方程的根
由于函数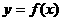 的零点就是方程
的零点就是方程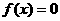 的根,所以在研究方程的有关问题,如:比较方程根的大小、确定方程根的分布、证明根的存在性等时,都可以将方程问题转化为函数问题,借助函数的零点,结合函数的图象加以解决。
的根,所以在研究方程的有关问题,如:比较方程根的大小、确定方程根的分布、证明根的存在性等时,都可以将方程问题转化为函数问题,借助函数的零点,结合函数的图象加以解决。
例2已知函数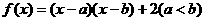 ,若
,若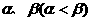 是方程
是方程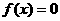 的两个根,则实数
的两个根,则实数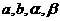 之间的大小关系是
( )
之间的大小关系是
( )
A.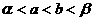 B.
B.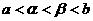 C.
C.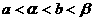 D.
D.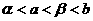
解:令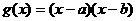 ,则函数
,则函数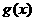 的两个零点是
的两个零点是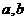 。
。
因为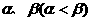 是方程
是方程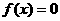 的两个根,
的两个根,
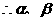 函数
函数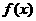 的两个零点。
的两个零点。
而函数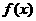 的图象是由函数
的图象是由函数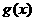 的图象向上平移两个单位得到的,
的图象向上平移两个单位得到的,
 结合图象可知:
结合图象可知: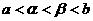 ,故选B。
,故选B。
例3已知关于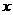 的方程
的方程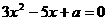 的两根
的两根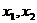 满足
满足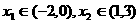 ,求实数
,求实数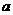 的取值范围。
的取值范围。
解:依题意,关于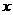 的方程
的方程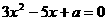 的两根
的两根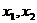 满足
满足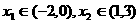 ,即函数
,即函数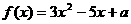 的两零点
的两零点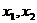 满足
满足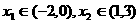 ,
,
 结合二次函数
结合二次函数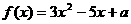 的图象可得:
的图象可得:
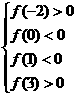 ,
,
即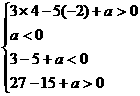 ,解得:
,解得: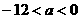 。
。
1、利用函数零点解不等式
二次函数的图象是连续的,当它通过零点(不是二重零点)时,函数值变号,并且在任意两个相邻的变号零点之间函数值保持同号,根据二次函数变号零点的这一性质,可以求解二次不等式。
例1二次函数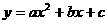 的部分对应值如下表:
的部分对应值如下表:
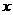
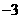
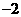
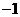

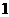
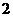
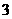
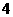
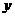
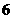

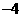
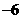
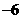
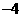

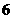
则不等式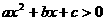 的解集是
的解集是 。
。
解:由表中数据可知函数的两个零点分别为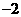 和
和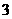 ,这两个零点将其余实数分为三个区间:
,这两个零点将其余实数分为三个区间: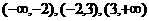 。
。
在区间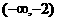 中取特殊值
中取特殊值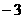 ,由于
,由于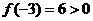 ,因此根据二次函数变号零点的性质可得:
,因此根据二次函数变号零点的性质可得:
当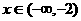 时,都有
时,都有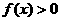 ;
;
当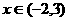 时,都有
时,都有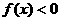 ;
;
当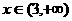 时,都有
时,都有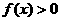 。
。
 不等式的解集为
不等式的解集为 。
。
例4 校办工厂现在年产值是15万元,如果每增加100元投资,一年可增加250元产值,那么总产值y(万元)与新增加的投资额x(万元)之间的函数关系是什么?如果增加1.5万元投资,年产值可达到多少?
解:依题意,得y=15+2.5x(x≥0).
当x=1.5万元时,y=15+2.5×1.5=15+3.75=18.75(万元).
答:(略)
由以上问题可知,当函数自变量的取值范围遇到实际问题时,应使实际问题有意义.因此,不管要求与否,求函数解析式时均应注明自变量的取值范围.
例3 某公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25米.由柱子顶端A处的喷水头向外喷水,水流向各个方向沿形状相同的抛物线落下.为使水流形状较为漂亮,要求设计成水流在离OA距离为1米处达到距水平最大高度2.25米.
如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不至落到池外?
分析:建立以OA所在直线为y轴,过点O垂直于OA的直线为x轴,O点为坐标原点的平面直角坐标系.设水流动的轨迹抛物线的顶点为B,水流落水与x轴交点为C,建立函数解析式求解.
解:由题意,知A(O,1.25)、B(1,2.25)、C(x,0).
设y=ax2+bx+c.∴=-x2+2x+1.25 .
当y=0时,x=2.5或x=-0.5(舍去).
∴池的半径至少要2.5米.
例1 某工厂现有甲种原料360千克、乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品,需用甲种原料4千克、乙种原料10千克,可获利润1200元.
(1)按要求安排A、B两种产品的生产件数,有哪几种方案?请你给设计出来;
(2)设生产A、B两种产品获总利润为y元,其中一种的生产件数为x,试写出y与x之间的函数关系式,并利用函数的性质说明(1)中哪种生产方案获总利润最大?最大利润是多少?
分析:列方程(组)解应用题的关键是找出包括应用题全部含义的相等关系,而函数型应用题的解题步骤与列方程(组)解应用题的步骤相类似,只是不一定列出相等关系(可以是相等或不等关系).
解:(1)设安排生产A种产品工件,则生产B种产品为(50-x)件.依题意,得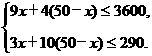 解此不等式组,得30≤x≤32.
解此不等式组,得30≤x≤32.
∵x为整数,∴x只能取30、31、32,相应的(50-x)的值为20、19、18.
∴生产方案有三种
第一种生产方案:生产A种产品30件、B种产品20件;
第二种生产方案:生产A种产品31件、B种产品19件;
第三种生产方案:生产A种产品32件、B种产品18件.
(2)设生产A种产品的件数为x,则生产B种产品的件数为50-x,依题意,得y=700x+1200(50-x).
∴y=500x+6000.其中x只能取30、31、32.
∵-500<0,∴此一次函数y随x的增大而减小.
∴当x=30时,y的值最大,
即按第一生产方案安排生产,获总利润最大.
最大利润为-500×30+6000=4500(元).
答:按第一生产方案安排生产获总利润最大,最大利润为4500元.
例2 某校校长暑假将带领该校市级三好学生去北京旅游,甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠.”乙旅行社说:“包括校长在内,全部按票价的6折(即按全票价的60%收费)优惠.”若全票价为240元,
(1)设学生数为x人,甲旅行社收费为y甲,乙旅行社收费为y乙,分别计算两家旅行社的收费(建立表达式);
(2)当学生数是多少时,两家旅行社的收费一样;
(3)就学生人数讨论哪家旅行社更优惠?
请同学自己给出解答.
提示:(1)y甲=120x+240,y乙=144x+144(x为正整数);
(2)x=4;
(3)x<4时,乙旅行社更优惠;当x>4时,甲旅行社更优惠.
5.已知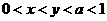 ,则有( )
,则有( )
 .
.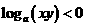
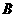 .
.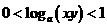
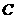 .
.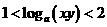
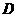 .
.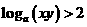
4.若函数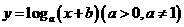 的图象过两点
的图象过两点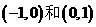 ,则( )
,则( )
 .
.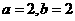
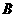 .
.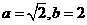
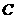 .
.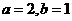
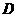 .
.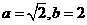
3.函数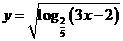 的定义域为( )
的定义域为( )
 .
.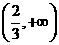
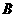 .
.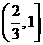
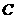 .
.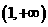
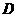 .
.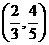
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com