
题目列表(包括答案和解析)
例3.求函数f(x)=x3+x2-2x-2的一个为正数的零点(精确到0.1)
分析:用二分法,要注意到初始区间的选取。
解:由于f(1)=-2<0,f(2)=6>0,可取区间[1,2]作为计算的初始区间。
用二分法逐次计算,列表如下:
|
端点(中点)坐标 |
计算中点的函数值 |
取区间 |
|
f(1)=-2<0 |
f(6)=6>0 |
[1,2] |
|
x1=(1+2)/2=1.5 |
f(x1)=0.625>0 |
[1,1.5] |
|
X2=(1+1.5)/2=1.25 |
f(x2)=-0.984<0 |
[1.25,1.5] |
|
X3=(1.25+1.5)/2=1.375 |
f(x3)=-0.260<0 |
[1.375,1.5] |
|
X4=(1.375+1.5)/2=1.438 |
f(x4)=0.165>0 |
[1.375,1.438] |
|
X5=(1.375+1.438)/2=1.4065 |
f(x5)=-0.052<0 |
|
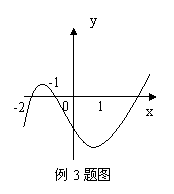
由上表的计算可知,区间[1.375,1.438]的长度小于0.1,所以这个区间的中点x5≈1.4可作为所求函数的一个正实数零点的近似值.函数f(x)=x3+x2-2x-2的图象如图.实际上还可用二分法继续算下去,进而得到这个零点精确度更高的近似值.
点评:给定精确度ε,用二分法求函数f(x)零点的近似值应该按课本P105的四个步骤进行.
例2.已知函数f (x)在其定义域上是单调函数,证明f(x)至多有一个零点.
分析:不妨设f(x)在R上是增函数,为证明f(x)=0至多有一个实根,考虑用反证法证明.
证明: 假设f(x)=0至少有两个不同的实根x1,x2,且不妨设x1<x2,
由题意得f(x1)=O,f(x2)=0, ∴f(x1)=f(x2) ①
∵f(x)在定义域上是单调菌数,不妨设为增函数,
由x1<x2,则f(x1)<f(x2)②
因此①②矛盾,假设不成立,故f(x)=0至多有一个零点.
例1.证明方程6-3x=2x在区间[1,2]内有唯一一个实数解,并求出这个实数解(精确到0.1).
证明: 设函数使f(x)=2x+3x-6.∵f(l)=-1<0,f(2)=4>0,又∵f(x)是增函数,所以函数f(x)=2x+3x-6在区间[1,2]有唯一的零点,则方程6-3x=2x在区间[1,2]有唯一一个实数解.
设该解为x0,则x0∈[1,2],取x1=1.5,f(1.5)=0.33>0,. F(1)·f(1.5)<0,∴ x0 ∈(1,1.5).
取x2=1.25,f(1.15)=0.128>0,f(1)·f(1.25)<0,∴x0∈(1,1.25).
取x3=1.125,f(1.125)=-0.44<0,f(1.125)·f(1.25)<0,∴x0∈(1.125,1.25).
取x4=1.187 5,f(1.187 5)=-0.16<0,f (1.187 5)·f(1.25)<0,∴.x0∈(1.187 5,1,25).
∵|1.25-1.87 5|=0.062 5<0.1,∴可取x0=1.2,则方程的实数解为x0=1.2.
点评:用二分法求方程实数解的思想是非常简明的、但是为了提高解的精确度,用二分法求方程实数解的过程又是较长的,有些计算不用计算工具甚至无法实施,所以需要借助科学计算器.
例6设x、y为实数,且满足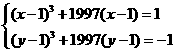 求x+y的值.
求x+y的值.
分析:若本题运用常规解法难以下手,但是若运用函数的单调性很容易求解.
当函数存在单调性时,根据(1)、(2)、(3)、(4)不难发现,则一定有:若f( )≠f(
)≠f( ),则
),则 ≠
≠ ;若f(
;若f( )=f(
)=f( ),则
),则 =
= .
.
解析 :由已知条件可得: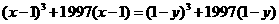 ,设函数f(x)=
,设函数f(x)=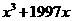 ,由于函数f(x)在R上单调递增,(证明略),且f(x-1)=f(1-y),所以x-1=1-y,即x+y=2.
,由于函数f(x)在R上单调递增,(证明略),且f(x-1)=f(1-y),所以x-1=1-y,即x+y=2.
点评:对定义的深刻理解,转化成解题中的深化运用,是简洁本题的关键.
例5已知函数f(x),x∈R的对称轴为x=2,当x>2时,f(x)为增函数.设a=f(1),b=f(4),c=f(-2),试确定的大小关系.
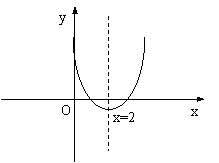 分析:欲比较三者的大小关系,只需根据对称性,画出示意图形(可以类比二次函数的图形),由图形结合单调性即可.
分析:欲比较三者的大小关系,只需根据对称性,画出示意图形(可以类比二次函数的图形),由图形结合单调性即可.
解析:因为函数f(x)的图像关于直线x=2对称.且x>2时f(x)为增函数,从而x<2时是减函数,从而可以肯定离对称轴x=2的距离越远的数,其函数值越大.
所以f(-2) >f(4) > f(1),即c>b>a.
点评:本题灵活的利用了函数的单调性进行大小的比较,结合图象形象直观的得到了结论,这是单调性定义应用的创意.
例4已知函数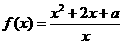 ,
,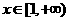 .
.
(1)当a=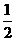 时,求函数f(x)的最小值;
时,求函数f(x)的最小值;
(2)若对任意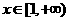 ,f(x)>0恒成立,试求实数a的取值范围.
,f(x)>0恒成立,试求实数a的取值范围.
分析:对于(1),将函数f(x)变形为f(x)= ,又定义可知
,又定义可知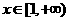 为单调增函数,对于(2)可以进合理的转化,变成二次函数的最值问题.
为单调增函数,对于(2)可以进合理的转化,变成二次函数的最值问题.
解析:(1)当a=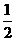 时,f(x)=
时,f(x)= ,根据例2的结论函数在
,根据例2的结论函数在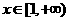 为单调增函数(证明略),故有f(x)≥f(1)=1+
为单调增函数(证明略),故有f(x)≥f(1)=1+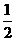 +2=
+2=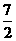 ,所以函数f(x)的最小值为
,所以函数f(x)的最小值为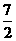 .
.
(2)在区间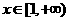 上
上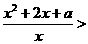 0恒成立,等价于
0恒成立,等价于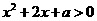 恒成立.
恒成立.
设g(x)=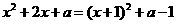 ,这是一个二次函数,在
,这是一个二次函数,在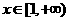 上单调递增,故有g (x)≥g(1)=3+a,g(x)的最小值为:3+a,只要3+a>0,故a>-3为所求.
上单调递增,故有g (x)≥g(1)=3+a,g(x)的最小值为:3+a,只要3+a>0,故a>-3为所求.
点评:课本中已知的函数的单调性在解题中可以直接利用,已经证明过的函数的单调性的结论有时也可以直接利用,因此,常见函数的单调性要熟练掌握,能够提高解题效率.
例3已知f(x)是定义在[-2,2]上的函数,且f(-x)=f(x),又f(x)在[0,2]上是减函数,且f(1-m) <f(m),求实数m的取值范围.
分析:由于f(x)在[0,2]上是减函数,考虑运用结论:(2)若 <
< ,则f(
,则f( )-f(
)-f( )>0
)>0 减函数解决问题.
减函数解决问题.
解析:∵f(-x)=f(x),∴f(x)=f(|x|),则f(1-m)= f(|1-m|),f(m)
=f(|m|),又f(1-m) -f(m)<0,∴f(|1-m|) -f(|m|)<0 ①,又f(x)在[0,2]上是减函数,则有(|1-m|-|m|)[ f(|1-m|) -f(|m|)]<0 ② ,由①②得|1-m|-|m|>0.从而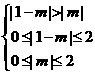 ,解得
,解得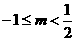 ,因此实数m的取值范围是
,因此实数m的取值范围是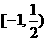 .
.
点评:抓住当f(-x)=f(x)时,得到f(x)=f(|x|)是解决本题的突破口.
例2已知函数f(x)=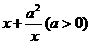 ,讨论函数在区间(0,+∞)上的单调性.
,讨论函数在区间(0,+∞)上的单调性.
分析:涉及讨论函数单调性的问题运用结论:(1)若 >
> ,则f(
,则f( )-f(
)-f( )>0
)>0 增函数;或(2)若
增函数;或(2)若 <
< ,则f(
,则f( )-f(
)-f( )>0
)>0 减函数比较方便.
减函数比较方便.
解析:任取0< <
< ,则f(
,则f( )-f(
)-f( )=
)=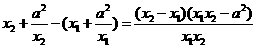 ,
,
当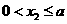 ,
,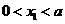 时,
时,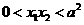 ,又
,又 <
< ,则
,则 -
- >0,所以f(
>0,所以f( )-f(
)-f( )=
)=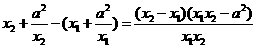 <0,所以f(
<0,所以f( )<f(
)<f( ),所以f(x)在(0,a
),所以f(x)在(0,a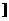 上是单调减函数.
上是单调减函数.
当a< <
< 时,
时,
 >
>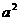 ,则f(
,则f( )-f(
)-f( )=
)=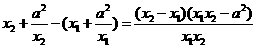 >0,f(
>0,f( )>f(
)>f( ),所以f(x)在[a,+∞
),所以f(x)在[a,+∞ 上是单调增函数.
上是单调增函数.
点评:一般地函数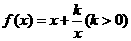 在
在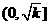 上为减函数,在
上为减函数,在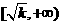 上为增函数,这个结论非常有用.
上为增函数,这个结论非常有用.
例1求证:函数f(x)=-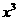 +1在(-∞,+∞)上是减函数.
+1在(-∞,+∞)上是减函数.
分析:考虑运用结论:(4)( -
- )[f(
)[f( )-f(
)-f( )]<0
)]<0 减函数进行证明,只需要进行因式分解变形.
减函数进行证明,只需要进行因式分解变形.
证明:在(-∞,+∞)上任取两个实数 、
、 ,且
,且 ≠
≠ ,则有(
,则有( -
- )[f(
)[f( )-f(
)-f( )]=(
)]=( -
- )(
)(
 -
-
 )=-(
)=-( -
- )
)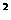 (
(
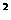 +
+
 +
+
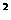 )=-(
)=-( -
- )
)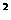 [
[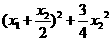 ]<0,即(
]<0,即( -
- )[f(
)[f( )-f(
)-f( )]<0,故函数f(x)=-
)]<0,故函数f(x)=-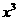 +1在(-∞,+∞)上是减函数.
+1在(-∞,+∞)上是减函数.
3.当两根都不在区间[α,β]内方程系数所满足的充要条件:
(1)两根分别在区间[α,β]之外的两旁时:
∵x1<α<β<x2,对应的函数f(x)的图象有下列两种情形(图3):
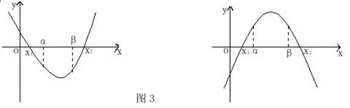
当a>0时的充要条件是:f (α)<0,f (β)<0
当a>0时的充要条件是:f (α)>0,f (β)>0
两种情形合并后的充要条件是:
af(α)<0,af(β)<0 ③
(2)两根分别在区间[α,β]之外的同旁时:
∵x1<x2<α<β或α<β<x1<x2,对应函数f(x)的图象有下列四种情形(图4):
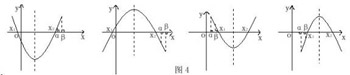
当x1<x2<α时的充要条件是:
Δ>0,-b/2a<α,af (α)>0 ④
当β<x1<x2时的充要条件是:
Δ>0,-b/2a>β,af (β)>0 ⑤
例9.已知方程x2+2Px+1=0有一个根大于1,有一个根小于1,则P的取值为 。
解:记f(x)=x2+2Px+1,则f(x)r的图象开口向上,当f(x)与x轴的两交点一个在(1,0)左方,另一个在(1,0)右方时,必有f(1)<0,即:
12+2P+1<0,即P<-1
所以P的取值为(-∞,-1)
例10.如果方程(1-m2)x2+2mx-1=0的两个根一个小于零,另一个大于1,试确定m的范围。
解:令f(x)=(1-m2)x2+2mx-1,根据题设条件,f(x)的图形是下列两种情形之一(图5):
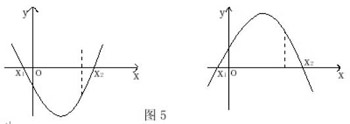
得充要条件:(1-m2)f(0)<0,(1-m2)f(1)<0;即1-m2>0,(1-m2)(2m-m2)<0
解得:-1<m<0
例11.已知二次函数f(x)=ax2+bx+c(a≠0).若方程f(x)=x无实根,求证:方程f[f(x)]=x也无实根,(北京市1994年高中一年级数学竞赛复赛试题)。
证明:已知f(x)=ax2+bx+c(a≠0)
方程f(x)=x即f(x)-x=ax2+(b-1)x+c=0无实根,f(x)-x仍是二次函数,f(x)-x=0仍是二次方程,它无实根即Δ=(b-1)2-4ac<0
若a>0,则函数y=f(x)-x的图象在x轴上方,
∴y>0,即f(x)-x>0恒成立,即:f(x)>x对任意实数x恒成立。
∴对f(x),
有f(f(x))>f(x)>x恒成立
∴f(f(x))=x无实根。
若a<0,函数y=f(x)-x的图象在x轴下方
∴y<0,即f(x)-x<0恒成立,
∴对任意实数x,f(x)<0恒成立,
∴对实数f(x),有:f(f(x))<f(x)<x恒成立,
∴f(f(x))=x无实根。
综上可知,当f(x)=x无实根时,方程f(f(x))=x也无实根。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com