

题目列表(包括答案和解析)
4.(2009年高考浙江卷)某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
|
高峰时间段用电价格表 |
低谷时间段用电价格表 |
|
||
|
高峰月用电量 (单位:千瓦时) |
高峰电价 (单位:元/千瓦时) |
低谷月用电量 (单位:千瓦时) |
低谷电价 (单位:元/千瓦时) |
|
|
50及以下的部分 |
0.568 |
50及以下的部分 |
0.288 |
|
|
超过50至200的部分 |
0.598 |
超过50至200的部分 |
0.318 |
|
|
超过200的部分 |
0.668 |
超过200的部分 |
0.388 |
若某家庭5月份的高峰时间段用电量为200千瓦时,低谷时间段用电量为100千瓦时,则按这种计费方式该家庭本月应付的电费为________元
解析:高峰时段电费a=50×0.568+(200-50)×0.598=118.1(元).
低谷时段电费b=50×0.288+(100-50)×0.318=30.3(元).
故该家庭本月应付的电费为a+b=148.4(元).答案:148.4
3.偶函数f(x)在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,则方程f(x)=0在区间[-a,a]内根的个数是__________.
解析:由题意函数f(x)在区间[0,a](a>0)上是单调函数,且f(0)·f(a)<0,根据零点存在定理知:在区间[0,a]内函数f(x)一定存在惟一零点且f(0)≠0,又函数f(x)是偶函数,故其在[-a,0]也惟一存在一个零点,所以方程f(x)=0在区间[-a,a]内根的个数为2.答案:2
2.根据表格中的数据,可以判定方程ex-x-2=0的一个根所在的区间为___.
|
x |
-1 |
0 |
1 |
2 |
3 |
|
ex |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
|
x+2 |
1 |
2 |
3 |
4 |
5 |
解析:据题意令f(x)=ex-x-2,由于f(1)=e1-1-2=2.72-3<0,f(2)=e2-4=7.39-4>0,故函数在区间(1,2)内存在零点,即方程在相应区间内有根.
答案:(1,2)
1.已知函数f(x)=则函数f(x)的零点个数为________.
解析:只要画出分段函数的图象,就可以知道图象与x轴有三个交点,即函数的零点有3个.答案:3
19.已知一个等差数列的前10项和是310,前20项和是1220,试求其前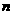 项和。
项和。
解:由题设: 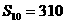
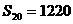 得:
得: 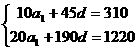
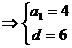 ∴
∴ 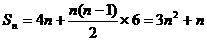
18、已知在数列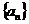 中,
中,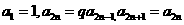 +d (
+d (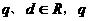 >0)
>0) .
.
(1)若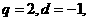 求
求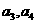 并猜测
并猜测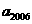 ;
;
(2)若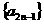 是等比数列,且
是等比数列,且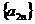 是等差数列,求
是等差数列,求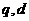 满足的条件.
满足的条件.
解:(1)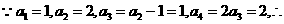 猜测
猜测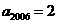 .
.
(2)由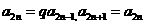
 ,得
,得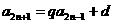 .
.
当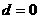 时,显然
时,显然 ,
,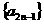 是等比数列.
是等比数列.
当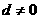 时,因为
时,因为 只有
只有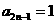 时,
时,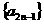 才是等比数列.
才是等比数列.
由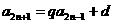 ,得
,得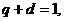 即
即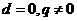 ,或
,或 .
.
由 得
得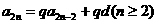 .
.
当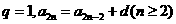 ,显然
,显然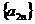 是等差数列,
是等差数列,
当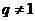 时,
时,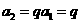 ,
,
只有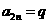 时,
时,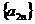 才是等差数列.
才是等差数列.
由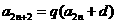 ,得
,得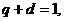 即
即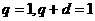 .
.
综上所述: .
.
17、已知数列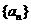 是首项为
是首项为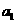 ,公差为
,公差为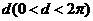 的等差数列,若数列
的等差数列,若数列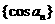 是等比数列,则其公比为( B )
是等比数列,则其公比为( B )

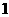
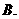


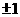

16、数列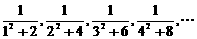 前n项的和等于
前n项的和等于 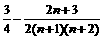 。
。
15、已知数列 的通项
的通项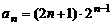 ,前n项和为
,前n项和为 ,则
,则 =
= 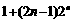 。
。
14、设 ,利用课本中推导等差数列前n项和的公式的方法,可求得:
,利用课本中推导等差数列前n项和的公式的方法,可求得: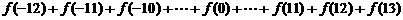 的值为
的值为 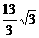
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com