

题目列表(包括答案和解析)
3、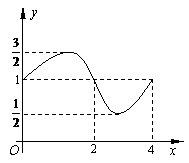 函数
函数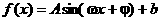 的图象如右,则
的图象如右,则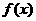 的解析式和
的解析式和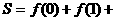
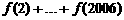 的值分别为
的值分别为
A.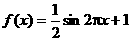 ,
, 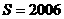
B.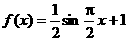 ,
, 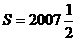
C.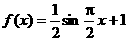 ,
, 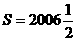
D.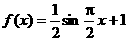 ,
, 
2、 函数
函数 的部分图象如右图所示,则
的部分图象如右图所示,则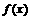 的解析式可能是
的解析式可能是
A.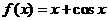
B.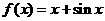
C.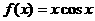
D.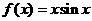
1、不等式sin2x>cos2x在区间(0,π)上的解集是
A、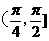 B、
B、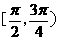 C、
C、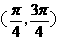 D、
D、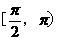
开放型问题是相对于中学课本中有明确条件和结论的封闭型问题而言的.这类问题的知识覆盖面大,综合性较强,灵活选择方法的要求较高,再加上题意新颖,构思精巧,具有相当的深度和难度.集合中的开放型问题问题大多是结论不定性开放型问题.
例3 设集合A = {(x,y)|y -x-1=
0 },集合B
={(x,y)|
4x
-x-1=
0 },集合B
={(x,y)|
4x +2x-2y+5 = 0 },集合C ={(x,y)| y = kx+b },是否存在k,b
+2x-2y+5 = 0 },集合C ={(x,y)| y = kx+b },是否存在k,b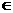 N,使得
N,使得 ?若存在,请求出k,b的值;若不存在,请说明理由.
?若存在,请求出k,b的值;若不存在,请说明理由.
解:因为 ,即
,即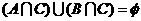 ,所以
,所以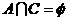 且
且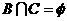 .
.
将y = kx+b代入y -x-1=
0,得k
-x-1=
0,得k x
x +(2kb-1)x+b
+(2kb-1)x+b -1= 0,
-1= 0,
因为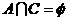 ,所以△
,所以△ = (2kb-1)
= (2kb-1) -4k
-4k ( b
( b -1)<0,即4k
-1)<0,即4k -4kb+1<0,若此不等式有解,应有16b
-4kb+1<0,若此不等式有解,应有16b -16>0,即b
-16>0,即b >1.①
>1.①
又将y = kx+b代入4x +2x-2y+5 = 0,得:4x
+2x-2y+5 = 0,得:4x +(2-2k)x+(5-2b) = 0,
+(2-2k)x+(5-2b) = 0,
因为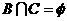 ,所以△
,所以△ = (2-2k)
= (2-2k) -4k(5-2b)<0,即k
-4k(5-2b)<0,即k -2k+8b-19<0,若此不等式有解,应有4-4(8b-19)>0,解得b<
-2k+8b-19<0,若此不等式有解,应有4-4(8b-19)>0,解得b<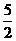 .②
.②
由不等式①、②及b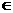 N,得b = 2.
N,得b = 2.
将b = 2代入由△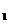 <0和△
<0和△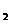 <0组成的不等式组,得
<0组成的不等式组,得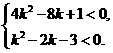 ,再注意到k
,再注意到k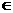 N,求得k = 1.
N,求得k = 1.
故存在自然数k = 1,b = 2使得 .
.
评析:在数学命题中,常以适合某种性质的结论“存在(肯定型)”、“不存在(否定型)”、“是否存在(讨论型)”等形式出现.“存在”就是有适合某种条件或符合某种性质的对象,对于这类问题无论用什么方法只要找出一个,就说明存在.“不存在”就是无论用什么方法都找不出一个适合某种已知条件或性质的对象,这类问题一般需要推理论证.“是否存在”结论有两种:一种是可能或存在;另一种是不存在,则需要说明理由.
解答集合问题时常常遇到这样的情况:解题过程中,解到某一步时,不能再以统一的方法、统一的形式继续进行,因为这时被研究的数学对象已包含了多种可能的情形,必须选定一个标准,根据这个标准划分成几个能用不同形式去解决的小问题,将这些小问题一一加以解决,从而使问题得到解决,这就是分类讨论的思想方法.
例2 设集合A = {x | x +4x = 0,x
+4x = 0,x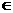 R},B = {x | x
R},B = {x | x +2(a+1)x+a
+2(a+1)x+a -1= 0,a
-1= 0,a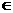 R,x
R,x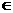 R },若
R },若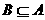 ,求实数a的取值范围。
,求实数a的取值范围。
分析:B A可分为B =
A可分为B =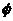 ,B
,B A,B = A三种情况讨论。
A,B = A三种情况讨论。
解:∵A = {0,-4},∴B A分以下三种情况:
A分以下三种情况:
⑴当B = A时,B= {0,-4},由此知:0和-4是方程x +2(a+1)x+a
+2(a+1)x+a -1= 0的两个根,由根与系数之间的关系,得:
-1= 0的两个根,由根与系数之间的关系,得:
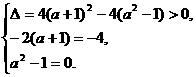
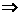 a = 1。
a = 1。
⑵当B A时,又可分为:
A时,又可分为:
①B =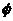 时,△= 4(a+1)
时,△= 4(a+1) -4(a
-4(a -1)<0,解得a<-1;
-1)<0,解得a<-1;
②B≠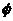 时,B = {0}或B = {-4},并且△= 4(a+1)
时,B = {0}或B = {-4},并且△= 4(a+1) -4(a
-4(a -1) = 0,解得a=-1,此时B = {0}满足题意。
-1) = 0,解得a=-1,此时B = {0}满足题意。
综合⑴、⑵知,所求实数a的值为a≤-1或a = 1。
评析:解分类讨论问题的实质是将整体化为部分来解决。对于含参数的计划问题,常需要对参数分类讨论。在分类时要注意“不重不漏”。由于空集是任何非空集合的真子集,空集必是非空集合的真子集,因此,B =φ时也满足B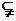 A.所以B
A.所以B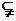 A中就应考虑B =
A中就应考虑B =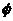 与B≠
与B≠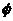 两种情况,就是说,正是空集
两种情况,就是说,正是空集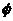 引法的分类讨论.
引法的分类讨论.
在解集合问题时,当一种集合的表达式不好入手时,可将其先转化为另一种形式.比如:将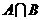 = B或将
= B或将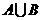 = A转化为
= A转化为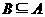 ,将
,将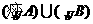 转化为
转化为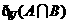 ,将
,将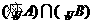 转化为
转化为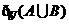 等.
等.
例1 已知M ={(x,y)| y = x+a},N
={(x,y)|
x +y
+y = 2},求使得
= 2},求使得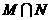 =
=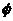 成立的实数a的取值范围。
成立的实数a的取值范围。
解: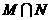 =
=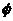 等价于方程组
等价于方程组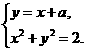 无解。
无解。
把y = x+a代入方程x +y
+y = 2中,消去y,得关于x的一元二次方程2x
= 2中,消去y,得关于x的一元二次方程2x +2ax+a
+2ax+a -2= 0。①
-2= 0。①
问题又转化为一元二次方程①无实根,即△= (2a) -4×2×(a
-4×2×(a -2)<0,由此解得a>2或a<-2。
-2)<0,由此解得a>2或a<-2。
故所求实数a的取值范围是{a | a>2或a<-2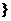 。
。
评析:在理解集合符号的基础上,准确地将集合语言转化为初中已学过的数学问题,然后用所学的知识和方法把问题解决.这种转化可以把抽象知识用简洁、准确的数学语言表达出来,提高解题效率.
20.已知双曲线的中心在坐标原点,焦点在x轴上,实轴长为2.一条斜率为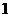 的直线l过右焦点F与双曲线交于A,B两点,以AB为直径的圆与右准线交于M,N两点.
的直线l过右焦点F与双曲线交于A,B两点,以AB为直径的圆与右准线交于M,N两点.
(1)若双曲线的离心率为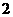 ,求圆的半径;
,求圆的半径;
(2)设AB的中点为H,若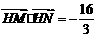 ,求双曲线的方程.
,求双曲线的方程.
解答:(1)设所求方程为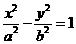 .由已知2a=2,∴a=1,又e=
.由已知2a=2,∴a=1,又e=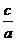 =2,∴c=2.
=2,∴c=2.
∴双曲线方程为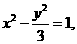 右焦点F(2,0),L;y=x-2,代入
右焦点F(2,0),L;y=x-2,代入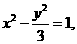 得
得
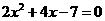 .设A(x1,y1),B(x2,y2),则
.设A(x1,y1),B(x2,y2),则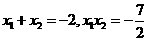 ,
,
∴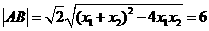 ,∴r=3.
,∴r=3.
(2)设双曲线方程为 L;y=x-2,代入并整理得
L;y=x-2,代入并整理得
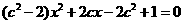 .
.
∴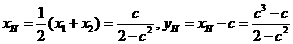 .
.
设半径为R,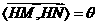 ,则
,则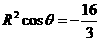 .
.
∵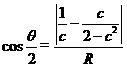 ,∴
,∴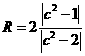 ,∴
,∴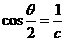 .
.
∴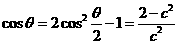 ,代入
,代入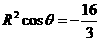 得:
得: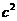 =3.
=3.
∴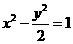 为所求.
为所求.
19.设椭圆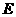 :
: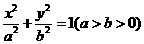 的左、右焦点分别为
的左、右焦点分别为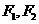 ,已知椭圆
,已知椭圆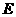 上任意一点
上任意一点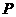 ,满足
,满足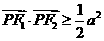 ,过
,过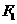 作垂直于椭圆长轴的弦长为3.
作垂直于椭圆长轴的弦长为3.
(1)求椭圆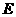 的方程;
的方程;
(2)若过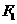 的直线交椭圆于
的直线交椭圆于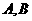 两点,求
两点,求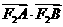 的取值范围.
的取值范围.
解:(1)设点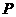
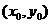 ,则
,则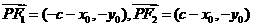 ,
,
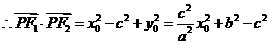
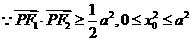
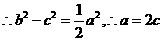 ,又
,又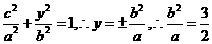 ,
,
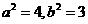 ,∴椭圆的方程为:
,∴椭圆的方程为: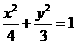
(2)当过 直线
直线 的斜率不存在时,点
的斜率不存在时,点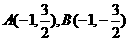 ,则
,则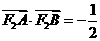 ;当过
;当过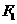 直线
直线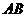 的斜率存在时,设斜率为
的斜率存在时,设斜率为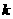 ,则直线
,则直线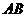 的方程为
的方程为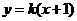 ,设
,设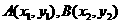
由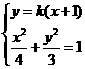 得:
得: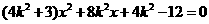
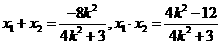
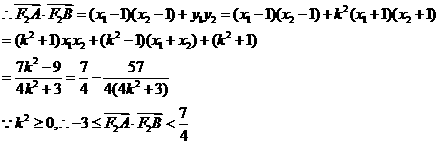
综合以上情形,得: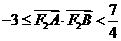
18. 在直角坐标平面上,O为原点,N为动点,|
在直角坐标平面上,O为原点,N为动点,|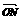 |=6,
|=6,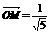
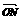 .过点M作MM1⊥y轴于M1,过N作
.过点M作MM1⊥y轴于M1,过N作
NN1⊥x轴于点N1,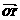 =
= +
+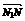 ,
,
记点T的轨迹为曲线C.
(Ⅰ)求曲线C的方程;
(Ⅱ)已知直线L与双曲线C1:5x2-y2=36
的右支相交于P、Q两点
(其中点P在第一象限),
线段OP交轨迹C于A,
若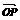 =3
=3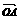 ,SΔPAQ=-26tan∠PAQ,
,SΔPAQ=-26tan∠PAQ,
求直线L的方程.
解:(Ⅰ)设T(x,y),点N(x1,y1),则N1(x1,0).又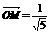
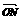 =(
=(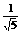 x1,
x1,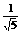 y1),∴M1(0,
y1),∴M1(0,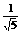 y1),
y1), =(
=(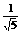 x1,0),
x1,0),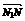 =(0,y1).于是
=(0,y1).于是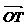 =
=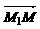 +
+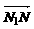 =(
=(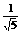 x1,y1),即(x,y)=(
x1,y1),即(x,y)=(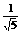 x1,y1).
x1,y1).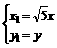 代入|
代入|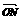 |=6,得5x2+y2=36.所求曲线C的轨迹方程为5x2+y2=36.
|=6,得5x2+y2=36.所求曲线C的轨迹方程为5x2+y2=36.
(II)设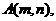 由
由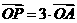 及
及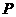 在第一象限得
在第一象限得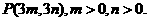
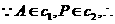
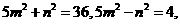 解得
解得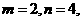 即
即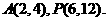 设
设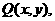 则
则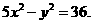 ①
①
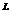 由
由 得
得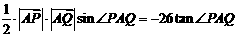 ,
,
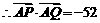 ,即
,即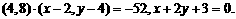 ②
②
联立①, ②,解得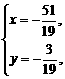 或
或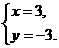 因点
因点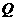 在双曲线C1的右支,故点
在双曲线C1的右支,故点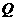 的坐标为
的坐标为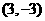 由
由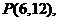
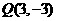 得直线
得直线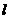 的方程为
的方程为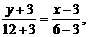 即
即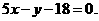
17.P是双曲线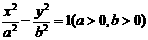 左支上一点,F1、F2分别是左、右焦点,且焦距为2c,则
左支上一点,F1、F2分别是左、右焦点,且焦距为2c,则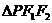 的内切圆的圆心横坐标为
的内切圆的圆心横坐标为 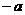 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com