
题目列表(包括答案和解析)
3.不等式|x+1|(2x-1)≥0的解集为( )
A.[ ,+∞)
B.(-∞,-1]∪[
,+∞)
B.(-∞,-1]∪[ ,+∞)
,+∞)
C.{-1}∪[ ,+∞)
D.[-1,
,+∞)
D.[-1, ]
]
答案:C
解析:当|x+1|=0即x=-1时不等式成立,
当|x+1|≠0时不等式等价于2x-1≥0,即x≥ .
.
2.不等式|x-1|+|x-2|≤3的最小整数解是( )
A.0 B.-1 C.1 D.2
答案:A
解析:将x=-1代入不等式知不成立,将x=0代入不等式成立,故选A.
1.不等式ax2+5x+c>0的解集为( ),那么a,c为( )
),那么a,c为( )
A.a=6,c=1 B.a=-6,c=-1
C.a=1,c=6 D.a=-1,c=-6
答案:B
解析:由题意得 为方程ax2+5x+c=0的两根是a<0.
为方程ax2+5x+c=0的两根是a<0.
故 =-
=-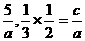 ,
,
∴a=-6,c=-1.
14.已知数列{an}满足:a1=2,an+1=2(1+ )2an.
)2an.
(1)求数列{an}的通项公式;
(2)设bn=(An2+Bn+C)·2n,试推断是否存在常数A,B,C,使对一切n∈N*都有an=bn+1-bn成立?说明你的理由;
(3)求证:a1+a2+a3+…+an≥2n+2-6.
(1)[解析]由已知an+1=2·(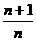 )2an,即
)2an,即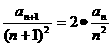 .
.
∴数列{ }是公比为2的等比数列,又
}是公比为2的等比数列,又 =2,∴
=2,∴ =2n.∴an=2n ·n2.
=2n.∴an=2n ·n2.
(2)[解析]∵bn+1-bn=[An2+(4A+B)n+2A+2B+C]·2n
若an=bn+1-bn恒成立,则n2=An2+(4A+B)n+2A+2B+C恒成立.
∴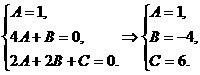 故存在常数A、B、C满足条件.
故存在常数A、B、C满足条件.
(3)证明:a1+a2+…+an=(b2-b1)+(b3-b2)+…+(bn+1-bn)=bn+1-b1
=[(n+1)2-4(n+1)+6]·2n+1-6=(n2-2n+3)·2n+1-6=[(n-1)2+2]·2n+1-6≥2n+2-6.
13.(2010全国大联考,22)已知正项数列{an} 满足a1=a(0<a<1=,且an+1=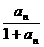 .求证:
.求证:
(1)0<an+1< ;
;
(2)an=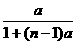 ;
;
(3) +…+
+…+ <1.
<1.
证明:(1)∵y= ,
,
∴函数y=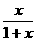 (0<x<1)是增?函数.
(0<x<1)是增?函数.
由已知an+1=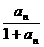 ,0<an<1,
,0<an<1,
∴0<an+1< .
.
(2)∵an+1=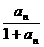 (n∈N*),
(n∈N*),
∴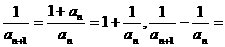 1(n∈N*),
1(n∈N*),
即数列{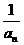 }是首项为
}是首项为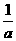 ,公差为1的等差数列.
,公差为1的等差数列.
∴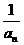 =
=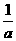 +(n-1),an=
+(n-1),an=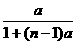 (n∈N*).
(n∈N*).
(3)由已知an=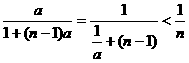 (∵0<a<1),
(∵0<a<1),
∴ +…+
+…+ +…+
+…+
=1- <1.
<1.
12.设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}(n∈N*)是等差数列,数列{bn-2}(n∈N*)是等比数列.
(1)求数列{an}和{bn}的通项公式;
(2)是否存在k∈N*,使ak-bk∈(0, )?若存在,求出k;若不存在,说明理由.
)?若存在,求出k;若不存在,说明理由.
[解析](1)由已知a2-a1=-2,a3-a2=-1,d=-1-(-2)=1.
∴an+1-an=(a2-a1)+(n-1)·1=n-3.
n≥2,an=(an-an-1)+(an-1-an-2+…+(a3-a2)+(a2-a1)+a1)
=(n-4)+(n-5)+…+(-1)+(-2)+6
=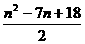 .
.
n=1也合适.
∴an=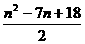 (n∈N*).
(n∈N*).
又b1-2=4,b2-2=2.即q= =
= ,
,
∴bn-2=(b1-2)·( )n-1,
)n-1,
即bn=2+8·( )n.
)n.
∴数列{an}{bn}的通项公式为:an=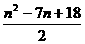 ,bn=2+(
,bn=2+( )n-3.
)n-3.
(2)设f(k)=ak-bk= k2-
k2- k+7-8·(
k+7-8·( )k=
)k= (k-
(k- )2+
)2+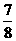 -8·(
-8·( )k.
)k.
当k≥4时 (k-
(k- )2+
)2+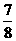 为k的增函数,-8·(
为k的增函数,-8·( )k也为k的增函数,
)k也为k的增函数,
而f(4)=  .
.
∴当k≥4时ak-bk≥ .
.
又f(1)=f(2)=f(3)=0,
∴不存在k,使f(k)∈(0, ).
).
11.已知An(n,an)为函数y1= 图象上的点,Bn(n,bn)为函数y2=x图象上的点,设?cn=an-bn,其中n∈N*.
图象上的点,Bn(n,bn)为函数y2=x图象上的点,设?cn=an-bn,其中n∈N*.
(1)求证:数列{cn}既不是等差数列也不是等比数列;
(2)试比较cn与cn+1的大小.
(1)证明:依题意,an= ,bn=n,cn=
,bn=n,cn= -n.
-n.
假设{cn}是等差数列,则2c2=c1+c3,
2( -2)=
-2)=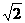 -1+
-1+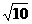 -3.
-3.
有2 =
=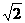 +
+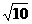 ,产生矛盾,∴{cn}不是等差数列.
,产生矛盾,∴{cn}不是等差数列.
假设{cn}是等比数列,则c22=c1c3,
即( -2)2=(
-2)2=(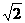 -1)(
-1)(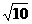 -3),有?21
-3),有?21 =47,产生矛盾.
=47,产生矛盾.
∴{an}也不是等比数列.
(2)[解析]∵cn+1= -(n+1)>0,
-(n+1)>0,
cn= -n>0,
-n>0,
∴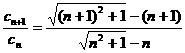 =
=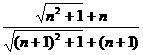 .
.
又∵0<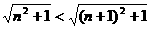 ,0<n<n+1,
,0<n<n+1,
∴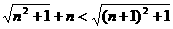 +n+1,
+n+1,
∴0<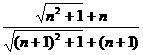 <1,
<1,
∴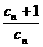 <1,即cn+1<cn.
<1,即cn+1<cn.
10.三个实数6、3、-1排成一行,在6和3之间插入两个实数,3和-1之间插入一个实数,使得这6个数中的前三个,后三个分别成等差数列,且插入的3个数本身顺次成等比数列,那么所插入的这3个数的和可能是:①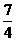 ;②3;③
;②3;③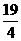 ;④7.其中正确的序号是(把正确的序号都填上).
;④7.其中正确的序号是(把正确的序号都填上).
[答案]①④
[解析]设插入的三个数为x、y、z,
则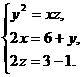 解得
解得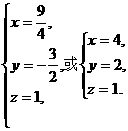
9.64个正数排成8行8列,如下所示
a11 a12 … a18
a21 a22 … a28
… … … …
a81 a82 … a88
在符号aij(1≤i≤8,1≤j≤8)中,i表示该数所在的行数,j表示该数所在的列数,已知每一行都成等差数列,而每一列都成等比数列(且每列公比都相等),a11= ,a24=1,a32=
,a24=1,a32=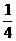 ,则aij的通项公式为aij=_________________.
,则aij的通项公式为aij=_________________.
[答案]j·( )i
)i
[解析]由题设第二行的公差为d,每一列的公比为q,则q= .
.
解得d=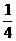 或d=
或d=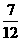 (舍,此时a21<0=),?q=
(舍,此时a21<0=),?q= ,
,
∴aij=a2j·( )i-2=[a24+(j-4)·
)i-2=[a24+(j-4)·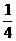 ]·(
]·( )i-2=j·(
)i-2=j·( )i.
)i.
8.一牧羊人赶着一群羊通过36个关口,每过一个关口,守关人将拿走当时羊的一半,然后退还一只,过完这些关口后,牧羊人只剩2只羊,牧羊人原来有_____________只羊.
[答案]2
解法一:(逆推)过最后一个关口有两只羊,则过第35个关口也是2只羊,依次类推,原来有2只羊.
解法二:设原有羊x只,则过第n个关口有an,则a1=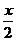 +1,an=
+1,an= an-1+1,∴an-2=
an-1+1,∴an-2= (an-1-2),{an-2}为等比数列,∴an=2+(x2-1)(
(an-1-2),{an-2}为等比数列,∴an=2+(x2-1)( )n-1.依题意,2+(
)n-1.依题意,2+(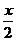 -1)(
-1)( )n-1=2
)n-1=2 x=2.
x=2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com