
题目列表(包括答案和解析)
13.已知全集U=R,A={x|x2-2x-8<0},B={x||x+3|>2},C={x|x2-4ax+3a2<0}.
(1)C (A∩B),求a的取值范围;
(A∩B),求a的取值范围;
(2)C (
(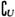 A)∩(
A)∩(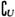 B),求a的取值范围.
B),求a的取值范围.
解析:A={x|-2<x<4},
B={x|x>-1或x<-5}.
∴A∩B={x|-1<x<4}.
当a>0时,C={x|a<x<3a};
当a=0时,C= ;
;
当a<0时,C={x|3a<x<a}.
(1)若C A∩B,则
A∩B,则
a=0或
∴a∈[- ].
].
(2)(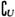 A)∩(
A)∩(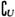 B)={x|-5≤x≤-2}.
B)={x|-5≤x≤-2}.
若C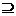 (
(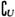 A)∩(
A)∩(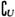 B),则
B),则
∴-2<a<- ,即a∈(-2,-
,即a∈(-2,- ).
).
12.已知|x-1|≤2且|x-a|≤2,求:
(1)当a<0时,求x的范围;
(2)若x的范围构成的集合是空集,求a的取值范围.
解析:|x-1|≤2 -1≤x≤3.
-1≤x≤3.
|x-a|≤2 -2+a≤x≤a+2.
-2+a≤x≤a+2.
(1)当a<0时,a+2<3,-2+a<-1.
①当a+2≥-1,即a≥-3时,x的取值范围为[a+2,3];
②当a+2<-1,即a<-3时,x的取值范围为?.
(2)由题意得 a+2<-1或-2+a>3.
故所求a的取值范围为a<-3或a>5.
11.(2010福建厦门一中模拟,17)解不等式:|x2-3x-4|<x+1.
解析:不等式等价于
解①得-1<x<5,解②得x<-1或x>3,
故原不等式的解集为{x|3<x<5}.
10.(2010江苏南通一模,14)若不等式|x-4|+|3-x|<a的解集是空集,则实数a的取值范围是_____________________.
答案:(-∞,1]
解析:由|x-4|+|3-x|≥|x-4+3-x|=1,故原不等式解集为空集,a的取值范围是(-∞,1].
9.若关于x的不等式a2-4+4x-x2>0成立时,不等式|x2-4|<1成立,则正数a的取值范围是_______.
答案:(0, -2]
-2]
解析:a2-4+4x-x2>0 2-a<x<2+a.|x2-4|<1
2-a<x<2+a.|x2-4|<1 -
- <x<
<x< ,由已知得
,由已知得 即0<a≤
即0<a≤ -2.
-2.
8.不等式 ≥
≥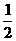 的解集是__________________.
的解集是__________________.
答案:[- ]
]
解析:∵|x|+2>0故原不等式为6-2|x|≥|x|+2即|x|≤ ,-
,- ≤x≤
≤x≤ .
.
7.(2010辽宁沈阳模拟,1)若不等式 -3≥0的解集是{x|-7≤x<-1},则实数a等于( )
-3≥0的解集是{x|-7≤x<-1},则实数a等于( )
A.0 B.-4 C.-6 D.-8
答案:B
解析:∵不等式 ≥0,
≥0,
即为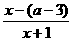 ≤0的解集为{x|-7≤x<-1},
≤0的解集为{x|-7≤x<-1},
∴a-3=-7.
∴a=-4.选B.
6.已知a>0,集合A={x||x+2|<a},B={x|ax>1},若A∩B≠ ,则实数a的取值范围是( )
,则实数a的取值范围是( )
A.(2,+∞) B.(0,1)
C.(0,1)∪(2,+∞) D.(0,1)∪(1,+∞)
答案:C
解析:A={x|-a-2<x<a-2}
当0<a<1时,B={x|x<0}又a-2<0故此时A B,则A∩B≠
B,则A∩B≠ .
.
当a>1时,B={x|x>0},
∵A∩B≠ ,∴a-2>0,即a>2.
,∴a-2>0,即a>2.
∴a的取值范围为(0,1)∪(2,+∞).
5.设U=R,A={x|mx2+8mx+21>0},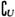 A=
A= ,则m的取值范围是( )
,则m的取值范围是( )
A.0≤m< B.m>
B.m> 或m=0
或m=0
C.m≤0
D.m≤0或m>
答案:A
解析:∵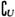 A=
A= ,
,
∴A=R,即mx2+8mx+21>0恒成立.
当m=0时,不等式恒成立.
当m≠0时,
则 0<m<
0<m< .
.
∴m的取值范围为[0, ).
).
4.设a>0,不等式|ax+b|<c的解集是{x|-2<x<1},则a∶b∶c等于( )
A.1∶2∶3 B.2∶1∶3
C.3∶1∶2 D.3∶2∶1
答案:B
解析:|ax+b|<c <x<
<x< ,故
,故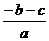 =-2,
=-2, =1即a∶b∶c=2∶1∶3.
=1即a∶b∶c=2∶1∶3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com