
题目列表(包括答案和解析)
5.等比数列{an}的各项都是正数,且a2,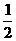 a3,a1成等差数列,则
a3,a1成等差数列,则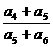 的值是( )
的值是( )
A.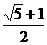 B.
B.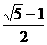
C.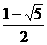 D.
D.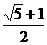 或
或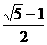
[答案]B
[解析]∵a3=a2+a1,
∴q2-q-1=0,q=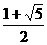 ,或q=
,或q=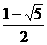 (舍).
(舍).
∴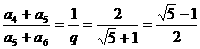 .
.
4.设f(x)是定义在R上恒不为零的函数,对任意实数x,y∈R,都有f(x)·f(y)=f(x+y),若a1=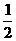 ,an=f(n)(n∈N*),则数列{an}前n项和Sn的取值范围是( )
,an=f(n)(n∈N*),则数列{an}前n项和Sn的取值范围是( )
A.[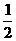 ,2)
B.[
,2)
B.[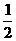 ,2]
,2]
C.[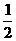 ,1)
D.[
,1)
D.[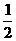 ,1]
,1]
[答案]C
[解析]因f(n+1)=f(1)·f(n),则an+1=a1·an=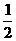 an,
an,
∴数列{an}是以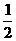 为首项,公比为
为首项,公比为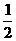 的等比数列.
的等比数列.
∴an=(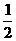 )n.
)n.
Sn=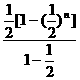 =1-(
=1-(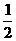 )n.
)n.
∵n∈N*,∴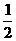 ≤Sn<1.
≤Sn<1.
3.数列{an}的前n项和Sn=3n+a,要使{an}是等比数列,则a的值为( )
A.0 B.1 C.-1 D.2
[答案]C
[解析]∵an=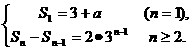
要使{an}成等比,则3+a=2·31-1=2·30=2,即a=-1.
2.一个公比q为正数的等比数列{an},若a1+a2=20,a3+a4=80,则a5+a6等于( )
A.120 B.240 C.320 D.480
[答案]C
[解析]∵a1+a2,a3+a4,a5+a6也成等比数列(公比为q2).
∴a5+a6=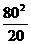 =320.
=320.
1.b2=ac,是a,b,c成等比数列的( )
A.充分不必要条件 B.必要非充分条件
C.充要条件 D.既不充分也不必要条件
[答案]B
[解析]因当b2=ac时,若a=b=c=0,则a,b,c不成等比数列;若a,b,c成等比,则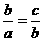 ,即b2=ac.
,即b2=ac.
13.(2010中科大附中模拟,19)等差数列{an}是递增数列,前n项和为Sn,且a1,a3,a9成等比数列,S5=a52;
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=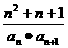 ,求数列{bn}的前99项的和.
,求数列{bn}的前99项的和.
[解析](1)设数列{an}公差为d(d>0),
∵a1,a3,a9成等比数列,
∴a32=a1a9,
(a1+2d)2=a1(a1+8d),d2=a1d. ①
∵d≠0,∴a1=d.
∵Sn=a52,
∴5a1+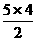 ·d=(a1+4d)2.
②
·d=(a1+4d)2.
②
由①②得:
a1=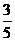 d=
d=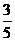 ,
,
∴an=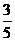 +(n-1)×
+(n-1)×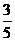 =
=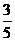 n.
n.
bn=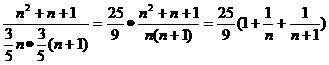 .
.
∴b1+b2+b3+…+b99
=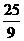 [99+(1-
[99+(1-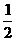 )+(
)+(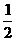 -
-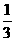 )+…+(
)+…+(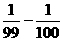 )]
)]
=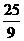 (100-
(100-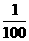 )=
)=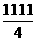 .
.
12.(2010湖北黄冈中学模拟,17)已知等比数列{an}中,a1=64,公比q≠1,a2,a3,a4又分别是某等差数列的第7项,第3项,第1项.
(1)求an;
(2)设bn=log2an,求数列{|bn|}的前n项和Tn.
[解析](1)依题意有a2-a4=3(a3-a4),
即2a4-3a3+a2=0,2a1q3-3a1q2+a1q=0,
即2q2-3q+1=0.∵q≠1,∴q=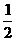 .
.
故an=64×(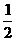 )n-1,
)n-1,
(2)bn=log2[64×(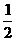 )n-1]=log227-n=7-n,
)n-1]=log227-n=7-n,
∴|bn|=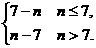
n≤7时,Tn=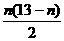 ;n>7时,
;n>7时,
Tn=T7+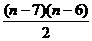
=21+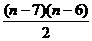 ,
,
故Tn=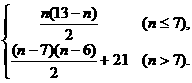
11.求a+2a2+3a3+…+nan.
[解析]设S=a+2a2+3a3+…+nan.
若a=0,则S=0;
若a=1,则S=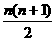 ;
;
若a≠0,且a≠1,则S=a+2a2+3a3+…+nan, ①
aS=a2+2a3+…+(n-1)an+na n+1 ②
①-②得
(1-a)S=a+a2+…+an-nan+1
=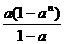 -nan+1.
-nan+1.
∴S=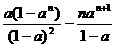 .
.
10.数列{an}满足a1=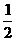 ,a1+a2+…+an=n2an,则an=_______________.
,a1+a2+…+an=n2an,则an=_______________.
[答案]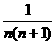 (n∈N*)
(n∈N*)
[解析]∵a1+a2+…+an=n2an ①
∴a1+a2+…+an+an+1=(n+1)2·an+1. ②
②-①得
∴an+1=(n+1)2an+1-n2an,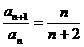 .
.
∴an=a1·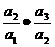 ·…·
·…·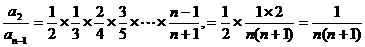 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com