11.{a_n}是等差数列，公差d＞0，S_n是{a_n}的前n项和，已知a₂a₃=40,S₄=26.

(1)求数列{a_n}的通项公式a_n；

(2)令b_n=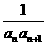，求数列{b_n}的所有项之和T.

[解析](1)S₄=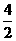(a₁+a₄)=2(a₂+a₃)=26.

又∵a₂a₃=40,d＞0，

∴a₂=5,a₃=8,d=3.

∴a_n=a₂+(n-2)d=3n-1.

(2)b_n==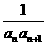

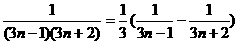
T_n=.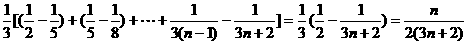

10.数列1,2+3,4+5+6,7+8+9+10,…,的一个通项公式a_n=__________________.

[答案]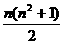

[解析]前n项一共有1+2+3+…+n=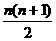个自然数,设S_n=1+2+3+…+n=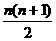,则

a_n=.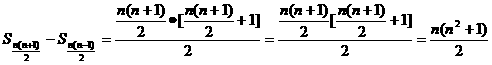

9.设f(x)=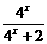,利用课本中推导等差数列前n项和方法,求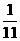f()+f()+…+f(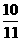)的值为_________________.

[答案]5

[解析]当x₁+x₂=1时,f(x₁)+f(x₂)

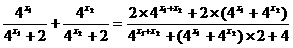==1.

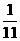设S=f()+f()+…+f(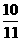),倒序相加有

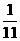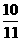2S=［f()+f()］+［f(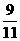)+f(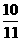)］+…+［f()+f(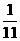)］=10.

即S=5.

8.黑白两种颜色的正六边形地面砖按如下图的规律拼成若干个图案:

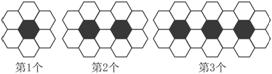
则第n个图案中有白色地面砖_____________块.

[答案]4n+2

[解析]每增加一块黑砖,则增加4块白砖,故白砖数构成首项为6,公差为4的等差数列,故a_n=6+4(n-1)=4n+2.

7.在等差数列{a_n}中,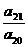＜-1,若它的前n项和S_n有最大值,则下列各数中是S_n的最小正数值的是(　　 )

A.S₁ B.S₃₈ C.S₃₉ D.S₄₀

[答案]C

[解析]因S_n有最大值,故d＜0,又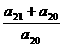＜0.

因a₂₁＜a₂₀,故a₂₀＞0,a₂₀+a₂₁＜0.

∴S₄₀=20(a₁+a₄₀)=20(a₂₀+a₂₁)＜0.

S₃₉=39a₂₀＞0,S₃₉-S₃₈=a₃₉＜0.

又S₃₉-S₁=a₂+a₃+…+a₃₉=19(a₂+a₃₉)=19(a₁+a₄₀)＜0,

故选C.

6.已知数列{a_n}的通项为a_n=26-2n,若要使此数列的前n项之和S_n最大,则n的值是(　　 )

A.12　　　　　　　　　 B.13　　　　　　　　　 C.12或13　　　　　　　 D.14

[答案]C

[解析]由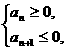得12≤n≤13,

故n=12或13.

5.已知数列{a_n}中,a₃=2,a₇=1,又数列{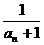}是等差数列,则a₁₁等于(　　 )

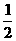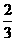A.0　　　　　　　　　 B.　　　　　　　　　 C.　　　　　　　　 D.-1

[答案]B

[解析]∵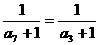+(7-3)d,

∴d=.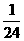

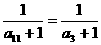∴+(11-3)d=,

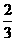a₁₁=.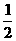

4.等差数列{a_n}的公差为d,前n项的和为S_n,当首项a₁和d变化时,a₂+a₈+a₁₁是一个定值,则下列各数中也为定值的是(　　 )

A.S₇ B.S₈ C.S₁₃ D.S₁₅

[答案]C

[解析]因a₂+a₈+a₁₁=3a₇,故a₇为定值.

又S₁₃==13a₇,

∴选C.

3.等差数列{a_n}中，若a₁+a₄+a₇=39,a₃+a₆+a₉=27，则前9项的和S₉等于(　　 )

A.66　　　　　　　　　　 B.99　　　　　　　　 C.144　　　　　　　　 D.297

[答案]B

[解析]a₁+a₄+a₇=39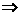a₄=13,a₃+a₆+a₉=27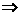a₆=9，

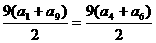S₉==99.

2.给出下列等式：(ⅰ)a_n+1-a_n=p(p为常数);(ⅱ)2a_n+1=a_n+a_n+2(n∈N^*);(ⅲ)a_n=kn+b(k,b为常数)则无穷数列{a_n}为等差数列的充要条件是(　　 )

A.(ⅰ)　　　　　　　　　　　　　　　　　　 B.(ⅰ)(ⅲ)

C.(ⅰ)(ⅱ)　　　　　　　　　　　　　　　　 D.(ⅰ)(ⅱ)(ⅲ)

[答案]D

[解析]易知三个都是，另外还有一个常见的是{a_n}的前n项和S_n=an²+bn，(a,b为常数).