
题目列表(包括答案和解析)
7.(2010全国大联考,12)一个机器猫每秒钟前进或后退1步,程序设计人员让机器猫以每前进3步后再后退2步的规律移动;如果将此机器猫放在数轴的原点上,面向正的方向,以1步的距离为1个单位长,令P(n)表示第n秒时机器猫所在的位置的坐标,且P(0)=0,那么下列结论中错误的是( )
A.P(3)=3 B.P(5)=1
C.P(101)=21 D.P(103)<P(104)
[答案]D
[解析]易知A、B正确,又机器猫每5秒钟实际向前进一步,故P(101)=P(5×20+1)=21, P(103)=P(20×5+3)=23,P(104)=P(20×5+3+1)=23-1=22,故选D.
6.若数列{an}前8项的值各异且an+8=an对任意n∈N*都成立,则下列数列中可取遍{an}前8项值的数列为( )
A.{a2k+1} B.{a3k+1} C.{a4k+1} D.{a6k+1}
[答案]B
[解析]∵2k+1,4k+1,6k+1只能取奇数,又周期为8,故排除A、C、D.选B.
5.数列{an}的前n项和为Sn=4n2-n+2,则该数列的通项公式为( )
A.an=8n+5(n∈N*)
B.an=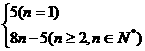
C.an=8n+5(n≥2) D.an=8n+5(n≥1)
[答案]B
[解析]a1=S1=4×12-1+2=5,排除A、C、D.
4.数列{an}中,a1=1,对所有的n≥2且n∈N*,都有a1a2…an=n2,则a3+a5等于( )
A.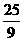 B.
B. C.
C.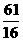 D.
D.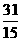
[答案]C
[解析]当n≥2时,an=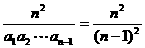 ,
,
故a3+a5=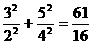 .
.
3.数列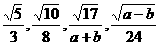 ,…中,有序数对(a,b)可以是( )
,…中,有序数对(a,b)可以是( )
A.(21,-5) B.(16,-1)
C.(-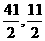 )
D.(
)
D.(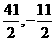 )
)
[答案]C
[解析]通项公式为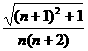 ,
,
故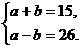
∴a=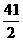 ,b=-
,b=-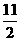 .
.
2.数列{an}中,a1=2,a2=5,an+1=an+2+an,则a6等于( )
A.-3 B.-4 C.-5 D.2
[答案]A
[解析]a3=a2-a1=3,a4=a3-a2=-2,a5=a4-a3=-5,a6=a5-a4=-3.
1.数列3,7,13,21,31,…的一个通项公式为( )
A.4n-1 B.n3-n2+n+2
C.n2+n+1 D.n(n-1)(n+2)
[答案]C
[解析]令n=3,排除A、B、D.
14.设{an}是正数组成的数列,其前n项和为Sn,且对于所有的正整数n,有an=2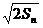 -2.
-2.
(1)写出数列{an}的三项;
(2)求数列{an}的通项公式,并写出推证过程;
(3)令bn=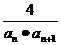 ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
[解析](1)由题意,当n=1时,有a1=2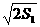 -2,S1=a1,
-2,S1=a1,
∴a1=2 -2,解得a1=2.
-2,解得a1=2.
当n=2时,有a2=2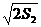 -2,S2=a1+a2,
-2,S2=a1+a2,
将a1=2代入,整理得(a2-2)2=16,
由a2>0,解得a2=6.
当n=3时,有a3=2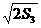 -2,S3=a1+a2+a3,
-2,S3=a1+a2+a3,
将a1=2,a2=6代入,整理得(a3-2)2=64,
由a3>0,解得a3=10.
所以该数列的前三项分别为2,6,10.
(2)由an=2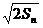 -2(n∈N*),整理得Sn=
-2(n∈N*),整理得Sn=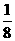 (an+2)2,
(an+2)2,
则Sn+1=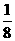 (an+1+2)2,
(an+1+2)2,
∴an+1=Sn+1-Sn=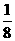 [(an+1+2)2-(an+2)2].
[(an+1+2)2-(an+2)2].
整理,得(an+1+an)(an+1-an-4)=0,
由题意知an+1+an≠0,∴an+1-an=4.
∴即数列{an}为等差数列,其中首项a1=2,公差d=4,
∴an=a1+(n-1)d=2+4(n-1).
即通项公式为an=4n-2(n∈N*).
(3)bn=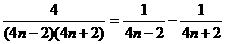 ,
,
Tn=b1+b2+…+bn
=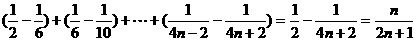 .
.
13.假设你在某公司打工,根据表现,老板给你两个加薪的方案:
(Ⅰ)每年年末加1 000元;
(Ⅱ)每半年结束时加300元.请你选择.
(1)如果在该公司干10年,问两种方案各加薪多少元?
(2)对于你而言,你会选择其中的哪一种?
[解析]设方案一第n年年末加薪an,因为每年末加薪1 000元,则an=1 000n;设方案二第n个半年加薪bn,因为每半年加薪300元,则bn=300n.
(1)在该公司干10年(20个半年),方案(Ⅰ)共加薪S10=a1+a2+…+a10=55 000(元).
方案(Ⅱ)共加薪T20=b1+b2+…+b20=20×300+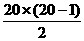 ×300=63 000元.
×300=63 000元.
(2)设在该公司干n年,两种方案共加薪分别为:
Sn=a1+a2+…+an=1 000×n+ ×1 000=500n2+500n,
×1 000=500n2+500n,
T2n=b1+b2+…+b20=2n×300+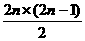 ×300=600n2+300n;
×300=600n2+300n;
令T2n≥Sn即600n2+300n>500n2+500n,解得,n≥2,当n=2时等号成立.
∴如果干3年以上(包括3年)应选择第二方案;如果只干2年,随便选;如果只干1年,当然选择第一方案.
12.已知f(x)=x2-2(n+1)x+n2+5n-7,
(1)设f(x)的图象的顶点的纵坐标构成数列{an},求证:{an}为等差数列;
(2)设f(x)的图象的顶点到x轴的距离构成{bn},求{bn}的前n项和.
(1)证明:f(x)=[x-(n+1)2]+3n-8,
∴an=3n-8.∵an-1-an=3,
∴{an}为等差数列.
(2)[解析]bn=|3n-8|,
当1≤n≤2时,bn=8-3n,b1=5.
Sn=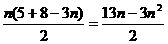 ;
;
当n≥3时,bn=3n-8.
Sn=5+2+1+4+…+(3n-8)
=7+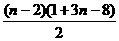
=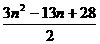 .
.
∴Sn=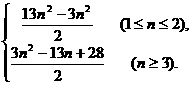
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com