
题目列表(包括答案和解析)
3.在一次数学实验中,运用图形计算器采集到如下一组数据:
|
x |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
|
y |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=a+bx C.y=a+logbx D.y=a+b/x
答案:A
解析:由x=0可排除C、D.x=0,y=1及x=1,y=2知:若y=a+bx,则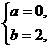 即y=2x,将其他数据代入近似满足;若y=a+bx,则a=1,b=1,即y=1+x,而x=-2时,y=-1不满足.
即y=2x,将其他数据代入近似满足;若y=a+bx,则a=1,b=1,即y=1+x,而x=-2时,y=-1不满足.
2.将进货单价为80元的商品按90元一个售出时,能卖出400个,已知该商品每个涨价1元,其销售量就减少20个,为了赚得最大利润,售价应定为( )
A.每个110元 B.每个105元
C.每个100元 D.每个95元
答案:D
解析:设该商品每个涨价a元,则利润y=(90+a-80)(400-20a)(a=0,1,2,…),即y=20(a+10)(20-a)=-20(a-5)2+4 500,?∴a=5即定价为95元时,y有最大值.
1.一种产品的成本原来为a元,计划在今后m年内使成本平均每年比上一年降低P%,则成本y与经过的年数x的函数关系式为( )
A.y=a(1-P%)x B.y=a(P%)x
C.y=a-(P%)x D.y=a(1+P%)x
答案:A
解析:成本每年比上一年降低P%,即每年成本是上一年的(1-P%)倍.
14.设f(x)=log2x-logx4(0<x<1),数列{an}的通项满足f(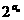 )=2n(n∈N*),问:{an}有没有最小的项?若有求出,若没有请说明理由.
)=2n(n∈N*),问:{an}有没有最小的项?若有求出,若没有请说明理由.
[解析]∵f(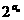 )=log2
)=log2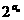 -log
-log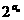 4=2n,
4=2n,
∴an-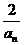 =2n,
=2n,
即an2-2nan-2=0,
解得:an=n±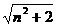 .
.
又∵0<x<1,∴0<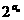 <1,
<1,
∴an<0,故an=n-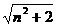 .
.
∴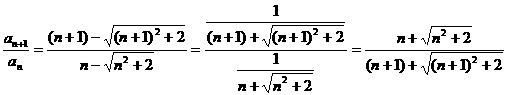 <1.
<1.
而an<0,∴an+1>an,故数列{an}是递增数列,其最小的项是a1=1-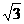 .
.
13.写出满足下列条件的数列的前5项,并归纳出通项公式.
(1)a1=0,an+1=an+(2n-1)(n∈N*);
(2)a1=1,an+1=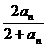 (n∈N*).
(n∈N*).
[解析](1)a1=0,a2=1,a3=4,a4=9,a5=16,an=(n-1)2.
(2)a1=1,a2=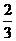 ,a3=
,a3=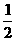 ,a4=
,a4=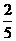 ,a5=
,a5=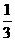 ,an=
,an=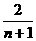 .
.
12.已知下面各数列{an}的前n项和Sn的公式,求{an}的通项公式.
(1)Sn=2n2-3n;(2)Sn=3n-2.
[解析](1)当n≥2时,an=Sn-Sn-1=2n2-3n-[2(n-1)2-3(n-1)]=4n-5.
当n=1时,a1=S1=-1满足上式,
∴an=4n-5.
(2)当n≥2时,an=Sn-Sn-1=(3n-2)-(3n-1-2)=2×3n-1,
当n=1时,a1=S1=3-2=1,
∴an=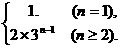
11.已知数列{an}的通项公式为an=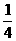 n2-
n2-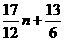 ,问
,问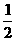 是否为数列{an}中的项?
是否为数列{an}中的项?
[解析]依题意,实际上要判断关于n的方程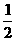 =
=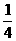 n2-
n2-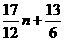 是否有正整数解.
是否有正整数解.
解方程得:n=4或n=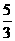 (舍),
(舍),
∴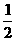 是数列{an}中的第四项.
是数列{an}中的第四项.
10.将正偶数按下表排成5列
|
|
第1列 |
第2列 |
第3列 |
第4列 |
第5列 |
|
第1行 |
|
2 |
4 |
6 |
8 |
|
第2行 |
16 |
14 |
12 |
10 |
|
|
第3行 |
|
18 |
20 |
22 |
24 |
|
… |
|
… |
28 |
26 |
|
那么2 006应在_________行,第____________列.
[答案]26 2
[解析]因2 006=2×1 003=2×4×25+2×3.
故2 006应第26行,由于是偶数行,故应在第2列.
9.(2010北京西城区模拟,14)定义运算符号:“Ⅱ”,这个符号表示若干个数相乘.例如:可将1×2×3×…×n记作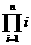 (n∈N*).记Tn=
(n∈N*).记Tn=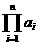 ,其中ai为数列{an}(n∈N*)中的第i项.
,其中ai为数列{an}(n∈N*)中的第i项.
(1)若an=2n-1,则T4=__________________;
(2)若Tn=n3(n∈N*),则an=______________.
[答案](1)105 (2)n=1时,a1=1;n≥2时,an=(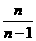 )2
)2
[解析](1)an=2n-1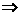 a1=1,a2=3,a3=5,a4=7.
a1=1,a2=3,a3=5,a4=7.
∴T4=1×3×5×7=105.
(2)Tn=n2,当n≥2时, =an.
=an.
当n=1时,a1=T1=1.
∴当n=1时,a1=1;当n≥2时,an=(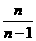 )2.
)2.
8.已知a1=1,an=1+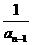 (n≥2,n∈N*),则a5=________________.
(n≥2,n∈N*),则a5=________________.
[答案]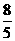
[解析]a2=1+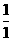 =2,a3=
=2,a3=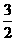 ,a4=
,a4=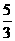 ,a5=
,a5=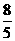 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com