
题目列表(包括答案和解析)
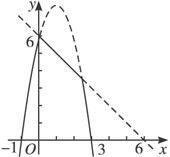
9.设f(x)表示-x+6和-2x2+4x+6中较小者,则函数的f(x)的最大值是_________________.
答案:6
解析:在同一坐标系中分别作出函数y=-x+6和y=-2x2+4x+6的图象如右图.显然,图中的实线部分为函数y=f(x)的图象.不难看出,当x=0时,f(x)有最大值为6.
8.若函数f(x)的图象经过点(0,-1),则函数f(x+3)的反函数的图象必经过点_______________.
答案:(-1,-3)
解析:由f(x)的图象经过点(0,-1),得?f(x+3)的图象经过点(-3,-1).∴f-1(x+3)的图象必经过点(-1,-3).
7.已知f(x)是R上的增函数,A(0,-1),B(3,1)是其图象上两个点,那么|f(x+1)|<1的解集是( )
A.(-∞,3) B.(-∞,2) C.(0,3) D.(-1,2)
答案:D
解析:-1<f(x+1)<1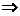 f(0)<f(x+1)<f(3)
f(0)<f(x+1)<f(3)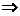 0<x+1<3,即-1<x<2.
0<x+1<3,即-1<x<2.
6.已知函数f(x)= 则函数y=f(1-x)的图象是图中的( )
则函数y=f(1-x)的图象是图中的( )
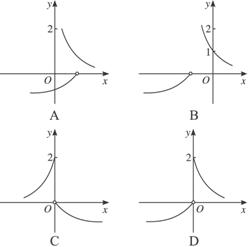
答案:D
解析:当1-x≤1即x≥0时,f(1-x)=21-x;
当1-x>1即x<0时,
f(1-x)=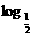 (1-x).
(1-x).
∴f(1-x)=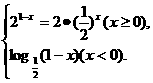 故选D.
故选D.
5.(2010北京东城区一模,7)设函数f(x)的图象关于点(1,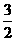 )对称,且存在反函数f-1(x),若f(3)=0,则f-1(3)等于( )
)对称,且存在反函数f-1(x),若f(3)=0,则f-1(3)等于( )
A.-1 B.1 C.-2 D.2
答案:A
解析:∵f(3)=0,即函数过点(3,0),又∵函数图象关于点(1,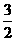 )对称,∴函数也过点?(-1,3),即f(-1)=3.∴f-1(3)=-1,故选A.
)对称,∴函数也过点?(-1,3),即f(-1)=3.∴f-1(3)=-1,故选A.
4.函数y=1(x+1)2的大致图象是( )
答案:C
解析:因x≠-1,故排除A、B.又当x>-1时,y=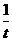 (t>0)递减,t=(x+1)2递增,故y=
(t>0)递减,t=(x+1)2递增,故y= 在(-1,+∞)上是减函数,排除D.选C.
在(-1,+∞)上是减函数,排除D.选C.
3.若函数f(x)=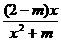 的图象如下图所示,则m的范围是( )
的图象如下图所示,则m的范围是( )
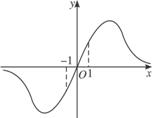
A.(-∞,-1) B.(-1,2)
C.(1,2) D.(0,2)
答案:D
解析:解法一:排除法,若m≤0,则函数f(x)=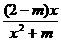 的定义域不为R,与图象信息定义域为R不符,故排除掉A、B.取m=1,f(x)=
的定义域不为R,与图象信息定义域为R不符,故排除掉A、B.取m=1,f(x)=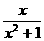 ,此函数当x=±1时,f(x)取得极值,与所给图形不符,排除C.选D.
,此函数当x=±1时,f(x)取得极值,与所给图形不符,排除C.选D.
解法二:显然f(x)为奇函数,又f(1)>0,f(-1)<0,即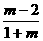 <0,解得-1<m<2.又f(x)取得最大值时,x=
<0,解得-1<m<2.又f(x)取得最大值时,x=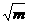 >1,
>1,
∴m>1,∴1<m<2.故选D.
2.将y=2x的图象向左平移一个单位,得到图象C1,再将C1向上平移一个单位得到图象C2,作出C2关于直线y=x的对称图象C3,则C3的解析式为( )
A.y=log2(x-1)-1 B.y=log2(x+1)+1
C.y=log2(x-1)+1 D.y=log2(x+1)-1
答案:A
解析:由题意知曲线C1的解析式为y=2x+1,C2的解析式为y=2x+1+1,又C2与C3关于直线y=x对称,
∴曲线C3的解析式即为y=2x+1+1的反函数,即所求解析式为y=log2(x-1)-1.故应选A.
1.要得到函数y=21-2x的图象,只需将函数y=( )x的图象( )
)x的图象( )
A.向左平移1个单位 B.向右平移1个单位
C.向左平移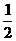 个单位
D.向右平移
个单位
D.向右平移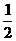 个单位
个单位
答案:D
解析:因y=21-2x=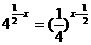 故选D.
故选D.
14.(2010华师附中模拟,20)设函数f(x)=2x+a·2-x-1(a为实数).
(1)若a<0,用函数单调性定义证明:y=f(x)在(-∞,+∞)上是增函数;
(2)若a=0,y=g(x)的图象与y=f(x)的图象关于直线y=x对称,求函数y=g(x)的解析式.
(1)证明:设任意实数x1<x2,则f(x1)-f(x2)=(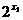 +a·
+a· -1)-(
-1)-(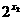 +a·
+a·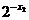 -1)
-1)
=(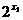 -
-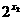 )+a(
)+a( -
-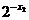 )=(
)=(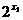 -
-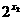 )·
)·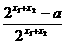 .
.
∵x1<x2,
∴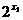 <
<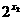 ,∴
,∴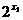 -
-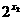 <0.
<0.
∵a<0,∴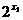 +x2-a>0.
+x2-a>0.
又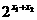 >0,∴f(x1)-f(x2)<0,
>0,∴f(x1)-f(x2)<0,
∴f(x)是增函数.
(2)解析:当a=0时,y=f(x)=2x-1,
∴2x=y+1,
∴x=log2(y+1),
y=g(x)=log2(x+1).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com