
题目列表(包括答案和解析)
1.若a>1,b>0,且ab+a-b=2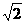 ,则ab-a-b的值为( )
,则ab-a-b的值为( )
A.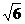 B.2或-2
C.-2
D.2
B.2或-2
C.-2
D.2
答案:D
解析:(ab+a-b)2=8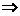 a2b+a-2b=6,
a2b+a-2b=6,
∴(ab-a-b)2=a2b+a-2b-2=4,
又ab>a-b(a>1,b>0),∴ab-a-b=2.
13.已知函数f(x)=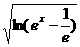 +ex.
+ex.
(1)求证:f(x)>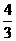 ;
;
(2)设A(x1,y1),B(x2,y2)是f(x)的图象上任意两点.求证:直线AB的斜率大于零.
证明:(1)先求f(x)的定义域.由ln(ex-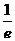 )≥0得ex-
)≥0得ex-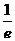 ≥1即ex≥
≥1即ex≥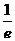 +1,
+1,
∴x≥ln(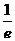 +1).求得f(x)的定义域为[ln(
+1).求得f(x)的定义域为[ln(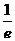 +1),+∞).
+1),+∞).
由于ln(ex-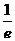 )及ex都是增函数,故f(x)在定义域内是增函数.
)及ex都是增函数,故f(x)在定义域内是增函数.
∴f(x)≥f[ln(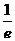 +1)]=
+1)]=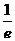 +1=
+1=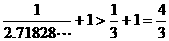 .
.
∴f(x)>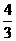 .
.
(2)设ln(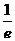 +1)<x1<x2,
+1)<x1<x2,
∵y=f(x)在定义域内是增函数,
∴y1<y2,故直线AB的斜率k=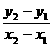 >0.
>0.
12.已知x满足2(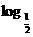 x)2+7
x)2+7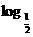 x+3≤0,求f(x)=(log2
x+3≤0,求f(x)=(log2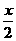 )·(log2
)·(log2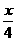 )的最小值和最大值.
)的最小值和最大值.
解析:∵2(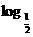 x)2+7
x)2+7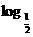 x+3=(2
x+3=(2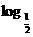 x+1)(
x+1)(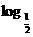 x+3)≤0,
x+3)≤0,
∴-3≤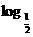 x≤-
x≤-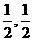 ≤log2x≤3.
≤log2x≤3.
令t=log2x,则t∈[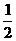 ,3],
,3],
∴f(x)=g(t)=(t-1)(t-2)=(t-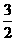 )2-
)2-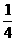 .
.
∵t∈[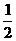 ,3],
,3],
∴f(x)∈[-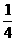 ,2].
,2].
∴f(x)的最小值和最大值分别为-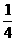 ,2.
,2.
11.设函数f(x)=loga(1-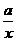 ),其中0<a<1.
),其中0<a<1.
(1)证明f(x)是(a,+∞)上的减函数;
(2)解不等式f(x)>1.
(1)证明:任取x1、x2∈(a+∞),且x1<x2,则f(x1)-f(x2)=loga(1-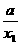 )-loga(1-
)-loga(1-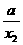 )=loga
)=loga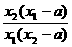 .
.
∵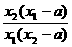 -1=
-1=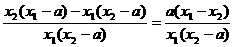 ,
,
∵0<a<1,a<x1<x2,
∴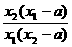 >0,且
>0,且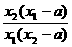 -1<0,
-1<0,
即0<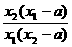 <1,
<1,
∴loga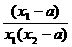 >0.
>0.
∴f(x1)>f(x2),∴f(x)是(a,+∞)上的减函数.
(2)解析:解法一:∵0<a<1,
∴f(x)>1 loga(1-
loga(1-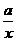 )>logaa
)>logaa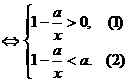
解不等式①得,x>a或x<0.
解不等式②得,0<x<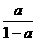 .
.
∵0<a<1,∴a<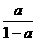 ,
,
∴原不等式解集为{x|a<x<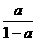 }.
}.
解法二:函数f(x)的定义域为{x|x>a或x<0}.
∵0<a<1,
∴当x<0时,1-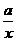 >1.
>1.
∴f(x)=loga(1-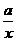 )<0,不合题意.
)<0,不合题意.
当x>a时,解方程f(x)=1,得x=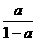 .
.
由(1)知f(x)是(a,+∞)上的减函数,
∴f(x)>1时,x<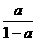 .
.
∵a<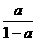 ,
,
∴原不等式解集为{x|a<x<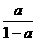 }.
}.
10.关于函数f(x)=lg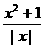 (x≠0,x∈R),有下列命题,其中正确命题的序号是__________(把你认为都正确的序号都填上).
(x≠0,x∈R),有下列命题,其中正确命题的序号是__________(把你认为都正确的序号都填上).
①函数y=f(x)的图象关于y轴对称;②当?x>0时,f(x)是增函数;当x<0时,?f(x)是减函数;
③函数f(x)的最小值是lg2;④当-1<x<0或x>1时,f(x)是增函数
答案:①③④
解析:设t=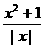 ,则t≥
,则t≥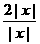 =2,
=2,
∴f(x)=lg2.
易证函数t=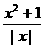 为偶函数,且x>0,t=x+
为偶函数,且x>0,t=x+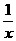 在(0,1)上递减,(1,?+∞)递增.故f(x)在(-1,0)或(1,+∞)递增.
在(0,1)上递减,(1,?+∞)递增.故f(x)在(-1,0)或(1,+∞)递增.
9.函数f(x)= 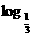 (x2-5x-6)的单调递减区间为________________.
(x2-5x-6)的单调递减区间为________________.
答案:(6,+∞)
解析:∵y=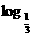 t递减,即求t=x2-5x-6的递增区间且t>0,故f(x)的递减区间为(6,+∞).
t递减,即求t=x2-5x-6的递增区间且t>0,故f(x)的递减区间为(6,+∞).
8.设方程lg2x+(lg2+lg3)·lgx+lg2·lg3=0的两根为x1、x2,那么x1·x2的值是________________.
答案:-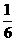
解析:lgx1+lgx2=-(lg2+lg3)lgx1x2=-lg6,x1·x2=-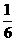 .
.
7.(2010江苏金陵中学模拟,5)设函数f(x)=1-x2+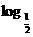 (x-1),则下列说法正确的是( )
(x-1),则下列说法正确的是( )
A.f(x)是增函数,没有最大值,有最小值
B.f(x)是增函数,没有最大值、最小值
C.f(x)是减函数,有最大值,没有最小值
D.f(x)是减函数,没有最大值、最小值
答案:D
解析:∵x>1,∴y1=1-x2在(1,+∞)递减.y2=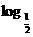 (x-1)在(1,+∞)上递减,∴f(x)在(1,+∞)上是减函数,且f(x)无最值.
(x-1)在(1,+∞)上递减,∴f(x)在(1,+∞)上是减函数,且f(x)无最值.
6.当a>1,在同一坐标系中,函数y=a-x和y=logax的图象是( )
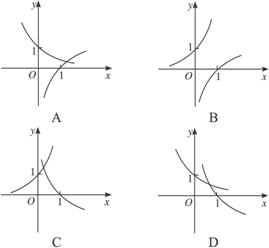
答案:A
解析:∵a>1,∴0<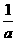 <1,故y=a-x=(
<1,故y=a-x=(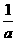 )x单调递减.故选A.
)x单调递减.故选A.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com