
题目列表(包括答案和解析)
4. 已知a、b为实数,且b>a>e,其中e为自然对数的底,求证:ab>ba.
证法一:∵b>a>e,∴要证ab>ba,只要证blna>alnb,设f(b)=blna-alnb(b>e),则
f′(b)=lna- .∵b>a>e,∴lna>1,且
.∵b>a>e,∴lna>1,且 <1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴ab>ba.
<1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴ab>ba.
证法二:要证ab>ba,只要证blna>alnb(e<a<b ,即证
,即证 ,设f(x)=
,设f(x)= (x>e),则f′(x)=
(x>e),则f′(x)= <0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
<0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
∴f(a)>f(b),即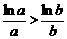 ,∴ab>ba.
,∴ab>ba.
3.已知 ,函数
,函数 的图象与函数
的图象与函数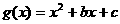 的图象相切。求b与c的关系式(用c表示b)
的图象相切。求b与c的关系式(用c表示b)
解:依题意令 ,得
,得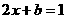 ,故
,故 .
.
由于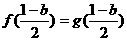 ,得
,得 。
。
点评:在由 得到
得到 ,就应想切线的交点必是在原两函数图象的交点,这是解决曲线切线问题的关键.
,就应想切线的交点必是在原两函数图象的交点,这是解决曲线切线问题的关键.
2. R 设圆内接等腰三角形的底边长为2x,高为h,那么h=AO+BO=R+
R 设圆内接等腰三角形的底边长为2x,高为h,那么h=AO+BO=R+ ,解得
,解得
x2=h(2R-h),于是内接三角形的面积为
 S=x·h=
S=x·h=
从而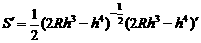

令S′=0,解得h= R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
R,由于不考虑不存在的情况,所在区间(0,2R)上列表如下:
|
h |
(0, R) R) |
 R R |
( ,2R) ,2R) |
|
S′ |
+ |
0 |
- |
|
S |
增函数 |
最大值 |
减函数 |
由此表可知,当x= R时,等腰三角形面积最大.
R时,等腰三角形面积最大.
2. 在半径为R的圆内,作内接等腰三角形,当底边上高为_________时它的面积最大.
1.A 导函数的正、负体现原函数的单调性,很明显
原函数的极大值点在y轴的右侧,再加上原函
数过原点,容易知道顶点在第Ⅰ象限.
1.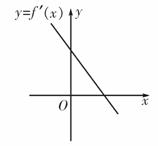 函数y=f(x)的图象过原点且它的导函数y=f′(x)
函数y=f(x)的图象过原点且它的导函数y=f′(x)
的图象是如图所示的一条直线,y=f(x)的图象的
顶点在 ( )
A.第Ⅰ象限 B.第Ⅱ象限
C.第Ⅲ象限 D.第Ⅳ象限
22. 如图,海中有一小岛,周围3.8海里内有暗礁。一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航行8海里到达C处,望见小岛B在北端东60°。若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?

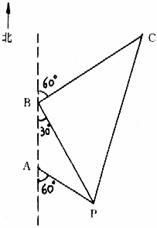
21. 如图,某海轮以30海里/小时的速度航行,在点A测得海面上油井P在南偏东60°,
向北航行40分钟后到达点B,测得油井P在南偏东30°,海轮改为北偏东60°
航向再航行80分钟到达点C,求P、C间的距离。
20. 在 中,已知
中,已知 ,
, ,
, .
.
(1)求 的值;
的值;
(2)求 的值.
的值.
(3)求 的面积
的面积
19. 已知△ABC的三个内角A,B,C,满足sinC=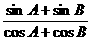 .
.
(1)判断△ABC的形状;
(2)设三边a,b,c成等差数列且S△ABC=6 cm2,求△ABC三边的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com