
题目列表(包括答案和解析)
1 下列四个结论:
下列四个结论:
⑴两条直线都和同一个平面平行,则这两条直线平行
⑵两条直线没有公共点,则这两条直线平行
⑶两条直线都和第三条直线垂直,则这两条直线平行
⑷一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行
其中正确的个数为( )
A
 B
B
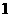 C
C
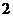 D
D
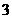
2 下面列举的图形一定是平面图形的是( )
下面列举的图形一定是平面图形的是( )
A 有一个角是直角的四边形 B
有一个角是直角的四边形 B 有两个角是直角的四边形
有两个角是直角的四边形
C 有三个角是直角的四边形 D
有三个角是直角的四边形 D 有四个角是直角的四边形
有四个角是直角的四边形
3 垂直于同一条直线的两条直线一定( )
垂直于同一条直线的两条直线一定( )
A 平行
B
平行
B 相交 C
相交 C 异面
D
异面
D 以上都有可能
以上都有可能
 4
4 如右图所示,正三棱锥
如右图所示,正三棱锥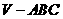 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,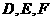 分别是
分别是 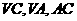 的中点,
的中点,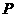 为
为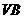 上任意一点,则直线
上任意一点,则直线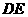 与
与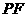 所成的角的大小是( )
所成的角的大小是( )
A
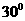 B
B
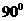 C
C
 D
D 随
随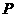 点的变化而变化
点的变化而变化
5 互不重合的三个平面最多可以把空间分成( )个部分
互不重合的三个平面最多可以把空间分成( )个部分
A
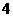 B
B
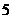 C
C
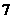 D
D
6 把正方形
把正方形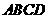 沿对角线
沿对角线 折起,当以
折起,当以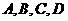 四点为顶点的三棱锥体积最大时,直线
四点为顶点的三棱锥体积最大时,直线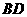 和平面
和平面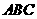 所成的角的大小为(
)
所成的角的大小为(
)
A
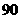 B
B
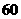 C
C
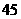 D
D

1 正方体
正方体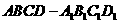 中,
中,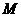 是
是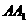 的中点
的中点 求证:平面
求证:平面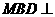 平面
平面
2 求证:三个两两垂直的平面的交线两两垂直
求证:三个两两垂直的平面的交线两两垂直
 3
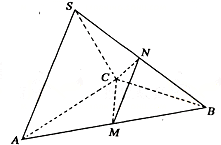
3 在三棱锥
在三棱锥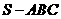 中,△
中,△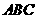 是边长为
是边长为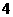 的正三角形,平面
的正三角形,平面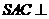 平面
平面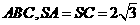 ,
,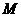 、
、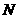 分别为
分别为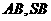 的中点
的中点
(Ⅰ)证明: ⊥
⊥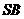 ;
;
(Ⅱ)求二面角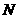 -
-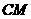 -
-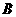 的大小;
的大小;
(Ⅲ)求点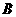 到平面
到平面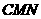 的距离
的距离
数学2(必修)
第二章 点、直线、平面之间的位置关系 [提高训练C组]
1 点
点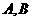 到平面
到平面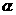 的距离分别为
的距离分别为 和
和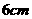 ,则线段
,则线段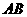 的中点
的中点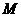 到
到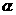 平面的
平面的
距离为_________________
2 从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为_______
从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为_______
3 一条直线和一个平面所成的角为
一条直线和一个平面所成的角为 ,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________
,则此直线和平面内不经过斜足的所有直线所成的角中最大的角是____________ 4
4 正四棱锥(顶点在底面的射影是底面正方形的中心)的体积为
正四棱锥(顶点在底面的射影是底面正方形的中心)的体积为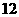 ,底面对角线的长为
,底面对角线的长为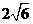 ,则侧面与底面所成的二面角等于___________________
,则侧面与底面所成的二面角等于___________________
5 在正三棱锥
在正三棱锥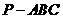 (顶点在底面的射影是底面正三角形的中心)中,
(顶点在底面的射影是底面正三角形的中心)中,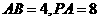 ,过
,过 作与
作与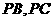 分别交于
分别交于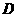 和
和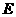 的截面,则截面
的截面,则截面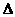
 的周长的最小值是________
的周长的最小值是________
1 设
设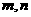 是两条不同的直线,
是两条不同的直线,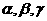 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若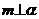 ,
,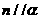 ,则
,则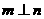 ②若
②若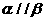 ,
,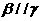 ,
,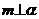 ,则
,则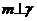
③若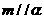 ,
,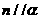 ,则
,则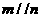 ④若
④若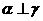 ,
,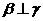 ,则
,则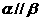
其中正确命题的序号是 ( )
A ①和② B
①和② B ②和③ C
②和③ C ③和④ D
③和④ D ①和④
①和④
2 若长方体的三个面的对角线长分别是
若长方体的三个面的对角线长分别是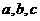 ,则长方体体对角线长为( )
,则长方体体对角线长为( )
A
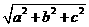 B
B
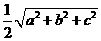
C
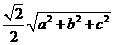 D
D
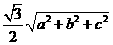
3 在三棱锥
在三棱锥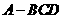 中,
中,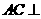 底面
底面 ,
,
则点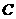 到平面
到平面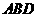 的距离是( )
的距离是( )
A
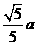 B
B
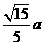 C
C
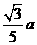 D
D
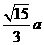
4 在正方体
在正方体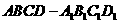 中,若
中,若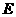 是
是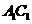 的中点,则直线
的中点,则直线 垂直于( )
垂直于( )
A
 B
B
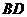 C
C
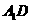 D
D
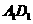
5 三棱锥
三棱锥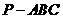 的高为
的高为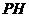 ,若三个侧面两两垂直,则
,若三个侧面两两垂直,则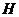 为△
为△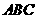 的( )
的( )
A 内心 B
内心 B 外心 C
外心 C 垂心 D
垂心 D 重心
重心
6 在四面体
在四面体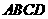 中,已知棱
中,已知棱 的长为
的长为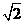 ,其余各棱长都为
,其余各棱长都为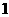 ,则二面角
,则二面角
 的余弦值为( )
的余弦值为( )
A
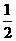 B
B
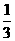 C
C
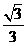 D
D
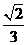
7 四面体
四面体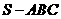 中,各个侧面都是边长为
中,各个侧面都是边长为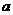 的正三角形,
的正三角形,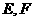 分别是
分别是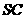 和
和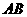 的中点,则异面直线
的中点,则异面直线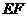 与
与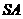 所成的角等于( )
所成的角等于( )
A
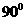 B
B
 C
C
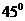 D
D
15. 小明、小华用4张扑克牌(分别是黑桃2、黑桃4,黑桃5、梅花5)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,小明先抽,小华后抽,抽出的牌不放回,各抽一张.
(1)若小明恰好抽到黑桃4;
①请绘制出这种情况的树状图;②求小华抽出的牌的牌面数字比4大的概率.
(2)小明、小华约定:若小明抽到的牌的牌面数字比小华的大,则小明胜,反之,则小明负,你认为这个游戏是否公平,说明你的理由.
14.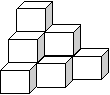 棱长为1 cm的小正方体组成如图所示的几何体,那么这个几何体的表面积是
棱长为1 cm的小正方体组成如图所示的几何体,那么这个几何体的表面积是
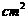 .
.
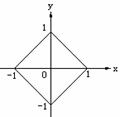
13. 设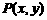 是下图中四边形内的点或四边形边界上的点(即x、y满足的约束条件),则
是下图中四边形内的点或四边形边界上的点(即x、y满足的约束条件),则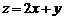 的最大值是__________.
的最大值是__________.
12.(文)圆C: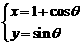 (
(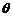 为参数)的普通方程为__________.
为参数)的普通方程为__________.
(理)由抛物线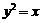 和直线
和直线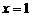 所围成图形的面积为_____________.
所围成图形的面积为_____________.
11. 已知单位向量i和j的夹角为60º,那么 (2j-i)•i= .
已知单位向量i和j的夹角为60º,那么 (2j-i)•i= .
10. 椭圆M: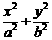 =1 (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且
=1 (a>b>0) 的左、右焦点分别为F1、F2,P为椭圆M上任一点,且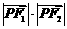 的最大值的取值范围是[2c2,3c2],其中
的最大值的取值范围是[2c2,3c2],其中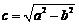 . 则椭圆M的离心率e的取值范围是( ).
. 则椭圆M的离心率e的取值范围是( ).
A.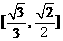 B.
B.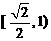 C.
C.
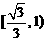 D.
D. 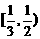
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com