
题目列表(包括答案和解析)
2、(北京市东城区2005年高三年级四月份综合练习)在△ABC中,a、b、c分别是角A、B、C的对边,且 (Ⅰ)求角B的大小(Ⅱ)若
(Ⅰ)求角B的大小(Ⅱ)若 ,求△ABC的面积.
,求△ABC的面积.
[思维分析]根据正弦定理和余弦定理将条件化为三角形边的关系或角的关系解答。
(Ⅰ)解法一:由正弦定理 得
得 将上式代入已知
将上式代入已知 即
即
 故A+B+C=
故A+B+C= ,
,
 为三角形的内角,
为三角形的内角, .
.
解法二:由余弦定理得 将上式代入
将上式代入 整理得
整理得
 为三角形的内角,
为三角形的内角, .
.
(Ⅱ)将 代入余弦定理
代入余弦定理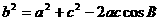 得
得


[知识点归类点拔]三角形中的三角函数问题一直是高考的热点内容之一。对正余弦定理的考查主要涉及三角形的边角互化(如判断三角形的形状等,利用正、余弦定理将条件中含有的边和角的关系转化为边或角的关系是解三角形的常规思路),三角形内的三角函数求值、三角恒等式的证明、三角形外接圆的半径等都体现了三角函数知识与三角形知识的交汇,体现了高考命题的原则。
[练28](1)(2004年北京春季高考)在 中,a,b,c分别是
中,a,b,c分别是 的对边长,已知a,b,c成等比数列,且
的对边长,已知a,b,c成等比数列,且 ,求
,求 的大小及
的大小及 的值。
的值。
答案: ,
,
(2)(2005天津)在△ABC中,∠A、∠B、∠C所对的边长分别为a、b、c,设a、b、c满足条件 和
和 。求∠A和
。求∠A和 的值。
的值。
答案: ,
,
[易错点29]含参分式不等式的解法。易对分类讨论的标准把握不准,分类讨论达不到不重不漏的目的。
例29、解关于x的不等式 >1(a≠1).
>1(a≠1).
[易错点分析]将不等式化为关于x的一元二次不等式后,忽视对二次项系数的正负的讨论,导致错解。
解:原不等式可化为: >0,即[(a-1)x+(2-a)](x-2)>0.
>0,即[(a-1)x+(2-a)](x-2)>0.
当a>1时,原不等式与(x-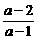 )(x-2)>0同解.若
)(x-2)>0同解.若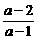 ≥2,即0≤a<1时,原不等式无解;若
≥2,即0≤a<1时,原不等式无解;若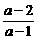 <2,即a<0或a>1,于是a>1时原不等式的解为(-∞,
<2,即a<0或a>1,于是a>1时原不等式的解为(-∞,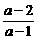 )∪(2,+∞).
)∪(2,+∞).
当a<1时,若a<0,解集为(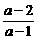 ,2);若0<a<1,解集为(2,
,2);若0<a<1,解集为(2,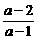 )
)
综上所述:当a>1时解集为(-∞,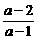 )∪(2,+∞);当0<a<1时,解集为(2,
)∪(2,+∞);当0<a<1时,解集为(2,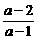 );当a=0时,解集为
);当a=0时,解集为 ;当a<0时,解集为(
;当a<0时,解集为(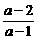 ,2).
,2).
[知识点分类点拔]解不等式对学生的运算化简等价转化能力有较高的要求,随着高考命题原则向能力立意的进一步转化,对解不等式的考查将会更是热点,解不等式需要注意下面几个问题:
(1)熟练掌握一元一次不等式(组)、一元二次不等式(组)的解法.
(2)掌握用序轴标根法解高次不等式和分式不等式,特别要注意因式的处理方法.
(3)掌握无理不等式的三种类型的等价形式,指数和对数不等式的几种基本类型的解法.
(4)掌握含绝对值不等式的几种基本类型的解法.
(5)在解不等式的过程中,要充分运用自己的分析能力,把原不等式等价地转化为易解的不等式.(6)对于含字母的不等式,要能按照正确的分类标准,进行分类讨论.
[练29](2005年江西高考)已知函数 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为
(1)求函数 的解析式;(2)设
的解析式;(2)设 ,解关于
,解关于 的不等式:
的不等式:
答案: ①当
①当 时,解集为
时,解集为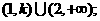 ②当
②当 时,不等式为
时,不等式为 解集为
解集为 ③当
③当 时,解集为
时,解集为
[易错点30]求函数的定义域与求函数值域错位
例30、已知函数 (1)如果函数
(1)如果函数 的定义域为R求实数m的取值范围。(2)如果函数
的定义域为R求实数m的取值范围。(2)如果函数 的值域为R求实数m的取值范围。
的值域为R求实数m的取值范围。
[易错点分析]此题学生易忽视对 是否为零的讨论,而导致思维不全面而漏解。另一方面对两个问题中定义域为R和值域为R的含义理解不透彻导致错解。
是否为零的讨论,而导致思维不全面而漏解。另一方面对两个问题中定义域为R和值域为R的含义理解不透彻导致错解。
解析:(1)据题意知若函数的定义域为R即对任意的x值
 恒成立,令
恒成立,令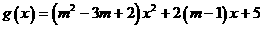 ,当
,当 =0时,即
=0时,即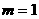 或
或 。经验证当
。经验证当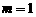 时适合,当
时适合,当 时,据二次函数知识若对任意x值函数值大于零恒成立,只需
时,据二次函数知识若对任意x值函数值大于零恒成立,只需 解之得
解之得 或
或 综上所知m的取值范围为
综上所知m的取值范围为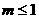 或
或 。
。
(2)如果函数 的值域为R即对数的真数
的值域为R即对数的真数 能取到任意的正数,令
能取到任意的正数,令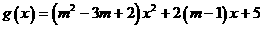 当
当 =0时,即
=0时,即 或
或 。经验证当
。经验证当 时适合,当
时适合,当 时,据二次函数知识知要使的函数值取得所有正值只需
时,据二次函数知识知要使的函数值取得所有正值只需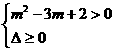 解之得
解之得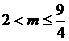 综上可知满足题意的m的取值范围是
综上可知满足题意的m的取值范围是 。
。
[知识点归类点拔]对于二次型函数或二次型不等式若二次项系数含有字母,要注意对字母是否为零进行讨论即函数是一次函数还是二次函数不等式是一次不等式还是二次不等式。同时通过本题的解析同学们要认真体会这种函数与不等式二者在解题中的结合要通过二者的相互转化而获得解题的突破破口。再者本题中函数的定义域和值域为R是两个不同的概念,前者是对任意的自变量x的值函数值恒正,后者是函数值必须取遍所有的正值二者有本质上的区别。
[练30]已知函数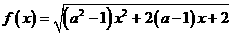 的定义域和值域分别为R试分别确定满足条件的a的取值范围。答案:(1)
的定义域和值域分别为R试分别确定满足条件的a的取值范围。答案:(1)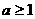 或
或 (2)
(2)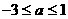 或
或
[易错点31]不等式的证明方法。学生不能据已知条件选择相应的证明方法,达不到对各种证明方法的灵活应用程度。
例31、已知a>0,b>0,且a+b=1.求证:(a+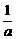 )(b+
)(b+ )≥
)≥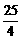 .
.
[易错点分析]此题若直接应用重要不等式证明,显然a+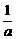 和 b+
和 b+ 不能同时取得等号,本题可有如下证明方法。
不能同时取得等号,本题可有如下证明方法。
证法一:(分析综合法)欲证原式,即证4(ab)2+4(a2+b2)-25ab+4≥0,即证4(ab)2-33(ab)+8≥0,即证ab≤ 或ab≥8.∵a>0,b>0,a+b=1,∴ab≥8不可能成立∵1=a+b≥2
或ab≥8.∵a>0,b>0,a+b=1,∴ab≥8不可能成立∵1=a+b≥2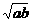 ,∴ab≤
,∴ab≤ ,从而得证.
,从而得证.
证法二:(均值代换法)设a=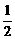 +t1,b=
+t1,b=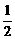 +t2.∵a+b=1,a>0,b>0,∴t1+t2=0,|t1|<
+t2.∵a+b=1,a>0,b>0,∴t1+t2=0,|t1|<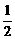 ,|t2|<
,|t2|<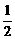
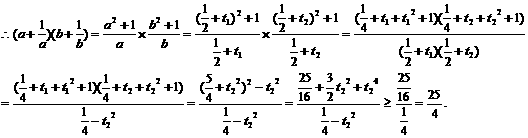 显然当且仅当t=0,即a=b=
显然当且仅当t=0,即a=b=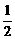 时,等号成立.
时,等号成立.
证法三:(比较法)∵a+b=1,a>0,b>0,∴a+b≥2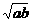 ,∴ab≤
,∴ab≤

证法四:(综合法)∵a+b=1, a>0,b>0,∴a+b≥2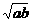 ,∴ab≤
,∴ab≤ .
.
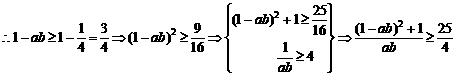

证法五:(三角代换法)∵ a>0,b>0,a+b=1,故令a=sin2α,b=cos2α,α∈(0, )
)
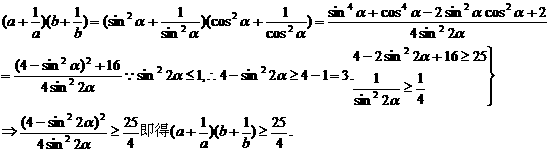
[知识点归类点拔]1.不等式证明常用的方法有:比较法、综合法和分析法,它们是证明不等式的最基本的方法.(1)比较法证不等式有作差(商)、变形、判断三个步骤,变形的主要方向是因式分解、配方,判断过程必须详细叙述;如果作差以后的式子可以整理为关于某一个变量的二次式,则考虑用判别式法证.
(2)综合法是由因导果,而分析法是执果索因,两法相互转换,互相渗透,互为前提,充分运用这一辩证关系,可以增加解题思路,开扩视野.
4.解答:由题意知:f(0)>0,f(1)<0,f(2)>0
 b>0,a+2b+1<0,a+b+2>0.
b>0,a+2b+1<0,a+b+2>0.
如图所示,A(-3,1),B(-2,0),C(-1,0).
又由所求量的几何意义知,值域分别为
(1)( ,1);(2)(8,17);(3)(-5,-4).
,1);(2)(8,17);(3)(-5,-4).
4.实系数方程f(x)=x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,求:
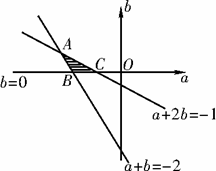 (1)
(1) 的值域;
的值域;
(2)(a-1)2+(b-2)2的值域;
(3)a+b-3的值域.
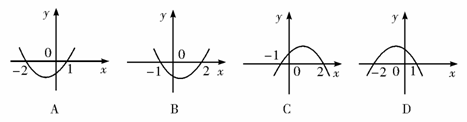
3.C 由已知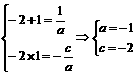 ,y=f(-x)=ax2+x-c,即y=-x2+x+2,其图象为C.
,y=f(-x)=ax2+x-c,即y=-x2+x+2,其图象为C.
3.如果不等式f(x)=ax2-x-c>0的解集为{x|-2<x<1},那么函数y=f(-x)的大致图象是 ( )
2.A||x|-1|+|y|=2可化为|y|=2-||x|-1|,即
y=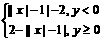
根据曲线|y|=2-||x|-1|的对称性可以作出图象
的变换,即由y=|x|的曲线向下平移一个单位,
得y=|x|-1,再将y轴下方的图象对折到x轴的
上方,可得y=||x|-1|,关于x轴对称可得y=-||x|-1|,
再向上平移两个单位可得y=2-||x|-1|,最后可得|y|=2-||x|-1|的图象如图所示,其面积为
(3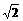 )2-2(
)2-2(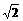 )2=14,故应选A.
)2=14,故应选A.
2.点集{(x,y)|||x|-1|+|y|=2}的图形是一条封闭的折线,这条封闭折线所围成的区域的面积是 ( )
 A.14
B.16
C.18
D.20
A.14
B.16
C.18
D.20
1.
Cf(x)=min{3+log x,log2x}=
x,log2x}= 分别解f(x)<2可得0<x<4或x>4,故应选C.
分别解f(x)<2可得0<x<4或x>4,故应选C.
1.若函数f(x)=min{3+log x,log2x},其中min{p,q}表示p,q两者中的较小者,则f(x)<2的解集为
( )
x,log2x},其中min{p,q}表示p,q两者中的较小者,则f(x)<2的解集为
( )
A.(0,4) B.(0,+∞) C. (0,4)∪(4,+∞) D ( ,+∞)
,+∞)
4.B由题意可知满足|PM|-|PN|=6的P的轨迹是双曲线的右支,根据“单曲型直线”的定义可知,就是求哪条直线与双曲线的右支有交点.故选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com