
题目列表(包括答案和解析)
2.一个正六面体的各个面和一个正八面体的各个面都是边长为a的正三角形,这样的两个多面体的内切球的半径之比是一个最简分数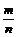 ,那么积m·n是 (
)
,那么积m·n是 (
)
A.6 B.3 C.54 D.24
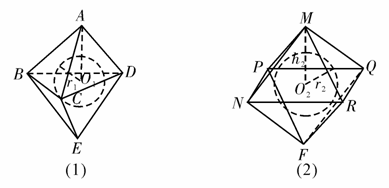
讲解:A。设六面体与八面体的内切球半径分别为r1与r2,再设六面体中的正三棱锥A-BCD的高为h1,八面体中的正四棱锥M-NPQR的高为h2,如图所示,则h1=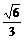 a,h2=
a,h2=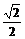 a.
a.
∵V正六面体=2·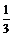 h1·S△BCD=6·
h1·S△BCD=6·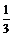 r1·S△ABC,∴r1=
r1·S△ABC,∴r1=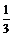 h1=
h1=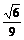 a.
a.
又∵V正八面体=2·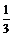 h2·S正方形NPQR=8·
h2·S正方形NPQR=8·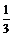 r2·S△MNP,
r2·S△MNP,
∴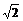 a3=2
a3=2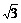 r2a2,r2=
r2a2,r2=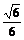 a,于是
a,于是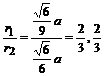 是最简分数,
是最简分数,
即m=2,n=3,∴m·n=6.故应选A.
1.有六根细木棒,其中较长的两根分别为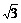 a、
a、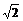 a,其余四根均为a,用它们搭成三棱锥,则其中两条较长的棱所在的直线的夹角的余弦值为
( )
a,其余四根均为a,用它们搭成三棱锥,则其中两条较长的棱所在的直线的夹角的余弦值为
( )
A.0
B.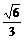 C.0或
C.0或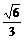 D.以上皆不对
D.以上皆不对
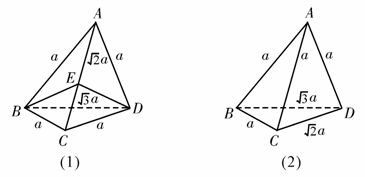
讲解:B。如图所示,本题共可作出两幅图,若不细辨别,可立即得C答案,但若对两幅图的存在性稍作回想,立即发现图实质上是一个陷阱,此图根本不存在.
取AC中点E,连结BE、ED,得BE=ED=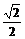 a,而BE+ED=
a,而BE+ED=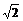 a<
a<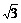 a=BD,故应排除(1),∴
a=BD,故应排除(1),∴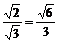 ,故应选B.
,故应选B.
3.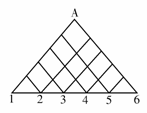 某游戏中,一个珠子从如图所示的通道由上至下滑下,
某游戏中,一个珠子从如图所示的通道由上至下滑下,
从最大面的六个出口出来,规定猜中出口者为胜.如果你
在该游戏中,猜得珠子从出口3出来,那么你取胜的概率为
( )
?A.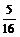 B.
B.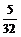 C.
C.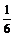 D.以上都不对
D.以上都不对
讲解:A.?珠子从出口1出来有C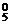 种方法,从出口2出来有C
种方法,从出口2出来有C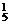 种方法,依次从出口i(1≤i≤6)有?C
种方法,依次从出口i(1≤i≤6)有?C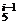 种方法,故取胜的概率为
种方法,故取胜的概率为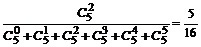 .
.
2.设a、b、m为整数(m>0),若a和b被m除得的余数相同,则称a和b对模m同余.记为a≡b(modm).已知a=1+C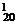 +C
+C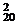 ·2+C
·2+C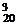 ·22+…+C
·22+…+C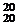 ·219,b≡a(mon10),则b的值可以是 ( ) A.2 015 B.2 011 C.2
008 D.2 006
·219,b≡a(mon10),则b的值可以是 ( ) A.2 015 B.2 011 C.2
008 D.2 006
讲解:B.?1+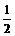 (C
(C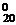 +C
+C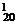 ·2+C
·2+C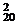 ·22+C
·22+C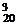 ·23+…+C
·23+…+C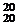 ·220-1)=1+
·220-1)=1+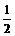 (320-1)=1+
(320-1)=1+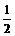 [(10-1)10-1]=1+
[(10-1)10-1]=1+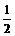
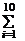 C
C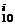 10(10-i)(-1)i,∵
10(10-i)(-1)i,∵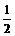
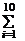 C
C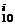 10(10-i)(-1)i中的每一项都能被10整除,∴a被10除的余数是1.
10(10-i)(-1)i中的每一项都能被10整除,∴a被10除的余数是1.
点评:b≡a(mon10)的含义是a、b被10除的余数相同,理解这一点才能明确代数式a的变形方向.
1.一圆形餐桌依次有A、B、C、D、E、F共有6个座位.现让3个大人和3个小孩入座进餐,要求任何两个小孩都不能坐在一起,则不同的入座方法总数为 ( )
?A.6 ?B.12 C.72 D.144
讲解:C.?大人的座位可能是A、C、E或B、D、F,故大人入座的方法数为2A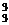 ;而小孩入座剩下座位的方法有A
;而小孩入座剩下座位的方法有A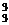 种,由分步计数法原理知方法总数为2A
种,由分步计数法原理知方法总数为2A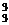 ·A
·A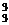 =72.
=72.
4. 设f(x)=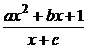 (a>0)为奇函数,且
|f(x)|min=2
(a>0)为奇函数,且
|f(x)|min=2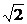 ,数列{an}与{bn}满足如下关系:
,数列{an}与{bn}满足如下关系:
a1=2,an+1=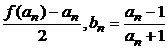 .
.
(1)求f(x)的解析表达式;
(2)证明:当n∈N+时,有bn≤(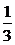 )n.
)n.
3. 等差数列{an}中有两项am和ak满足am=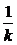 ,ak=
,ak=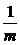 ,则该数列前mk项之和是
.
,则该数列前mk项之和是
.
2. 等差数列{an}的通项公式是an=1-2n,其前n项和为Sn,则数列{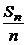 }的前11项和为 ( )
}的前11项和为 ( )
A.-45 B.-50 C.-55 D.-66
1.若等比数列{an}对一切正整数n都有Sn=2an-1,其中 Sn是{an}的前n项和,则公比q的值为 ( )
A.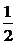 B.-
B.-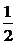 C.2
D.-2
C.2
D.-2
4.已知向量m=(cosθ,sinθ)和n=(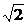 -sinθ,cosθ),θ∈[π,2π].
-sinθ,cosθ),θ∈[π,2π].
(1)求|m+n|的最大值;
(2)当|m+n|=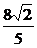 时,求cos(
时,求cos(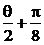 )的值.
)的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com