2．平面图形的翻折，要注意翻折前后的长度、角度、位置的变化，翻折前后在同一个三角形中的角度、长度不变

1．计算问题：

(1)空间角的计算步骤：一作、二证、三算

异面直线所成的角　 范围：0°＜θ≤90°　 方法：①平移法；②补形法.

直线与平面所成的角　 范围：0°≤θ≤90° 方法：关键是作垂线，找射影.

二面角　 方法：①定义法；②三垂线定理及其逆定理；③垂面法. 注：二面角的计算也可利用射影面积公式S′=Scosθ来计算

(2)空间距离

1)两点之间的距离；2)点到直线的距离；3)点到平面的距离；4)两条平行线间的距离；5)两条异面直线间的距离；6)平面的平行直线与平面之间的距离；7)两个平行平面之间的距离。

七种距离都是指它们所在的两个点集之间所含两点的距离中最小的距离。七种距离之间有密切联系，有些可以相互转化，如两条平行线的距离可转化为求点到直线的距离，平行线面间的距离或平行平面间的距离都可转化成点到平面的距离。

在七种距离中，求点到平面的距离是重点，求两条异面直线间的距离是难点。

求点到平面的距离：(1)直接法，即直接由点作垂线，求垂线段的长.(2)转移法，转化成求另一点到该平面的距离.(3)体积法.

求异面直线的距离：(1)定义法，即求公垂线段的长.(2)转化成求直线与平面的距离.(3)函数极值法，依据是两条异面直线的距离是分别在两条异面直线上两点间距离中最小的.

9．会用反证法证明简单的命题。如两直线异面。

主要思想与方法：

8．正多面体：掌握定义和正多面体的种数(是哪几个？)　　　　

　　　　　　　　　　　　　　。

掌握欧拉公式：V+F-E=2　 其中：V顶点数　E棱数　F面数

7．球的相关概念：S_球=4πR²　V_球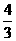＝πR³　球面距离的概念

6．棱锥

(1)棱锥的定义、正棱锥的定义(底面是正多边形，顶点在底面上的射影是底面的中心)

(2)相关计算：S_侧＝各侧面的面积和，V=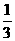Sh

5．棱柱

(1)掌握棱柱的定义、分类，理解直棱柱、正棱柱的性质。

(2)掌握长方体的对角线的性质。

(3)平行六面体→直平行六面体→长方体→正四棱柱→正方体这些几何体之间的联系和区别，以及它们的特有性质。

(4)S_侧＝各侧面的面积和。思考：对于特殊的棱柱，又如何计算？

(5)V=Sh 特殊的棱柱的体积如何计算？

4.平面与平面 (1)位置关系：平行、相交，(垂直是相交的一种特殊情况)

(2)掌握平面与平面平行的证明方法和性质。

(3)掌握平面与平面垂直的证明方法和性质定理。尤其是已知两平面垂直，一般是依据性质定理，可以证明线面垂直。

(4)两平面间的距离问题→点到面的距离问题→

(5)二面角。二面角的平面交的作法及求法：

①定义法，一般要利用图形的对称性；一般在计算时要解斜三角形；

②垂线、斜线、射影法，一般要求平面的垂线好找，一般在计算时要解一个直角三角形。

③射影面积法，一般是二面交的两个面只有一个公共点，两个面的交线不容易找到时用此法。

3.直线与平面

①位置关系：平行、直线在平面内、直线与平面相交。

②直线与平面平行的判断方法及性质,判定定理是证明平行问题的依据。

③直线与平面垂直的证明方法有哪些？

④直线与平面所成的角：关键是找它在平面内的射影，范围是{0⁰.90⁰}

⑤三垂线定理及其逆定理：每年高考试题都要考查这个定理. 三垂线定理及其逆定理主要用于证明垂直关系与空间图形的度量.如：证明异面直线垂直，确定二面角的平面角，确定点到直线的垂线。

2.空间两条直线的位置关系：平行、相交、异面的概念；

会求异面直线所成的角和异面直线间的距离；证明两条直线是异面直线一般用反证法。