
题目列表(包括答案和解析)
21.(1)选修4-2:矩阵与变换
变换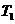 是逆时针旋转
是逆时针旋转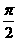 的旋转变换,对应的变换矩阵是
的旋转变换,对应的变换矩阵是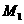 ;变换
;变换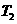 对应的变换矩阵是
对应的变换矩阵是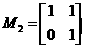 .
.
(1)求点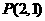 在变换
在变换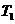 作用下的点
作用下的点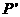 的坐标;
的坐标;
(2)求函数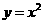 的图象依次在变换
的图象依次在变换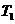 ,
,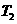 作用下所得曲线的方程.
作用下所得曲线的方程.

20.(本小题满分16分)
已知函数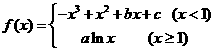 的图象过点
的图象过点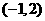 ,且在点
,且在点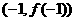 处的切线与直线
处的切线与直线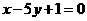 垂直.
垂直.
(1) 求实数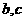 的值;
的值;
(2) 求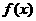 在
在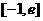 (
(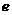 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;
(3) 对任意给定的正实数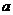 ,曲线
,曲线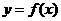 上是否存在两点
上是否存在两点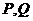 ,使得
,使得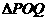 是以
是以 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在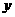 轴上?
轴上?
19.(本小题满分16分)
已知数列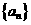 满足:
满足: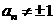 ,
,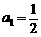 ,
,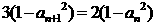 ,记数列
,记数列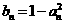 ,
,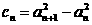 (
(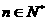 ).
).
(1)证明数列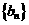 是等比数列;
是等比数列;
(2)求数列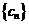 的通项公式;
的通项公式;
(3)是否存在数列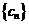 的不同项
的不同项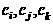 (
(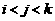 )使之成为等差数列?若存在请求出这样的不同项
)使之成为等差数列?若存在请求出这样的不同项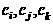 (
(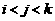 );若不存在,请说明理由.
);若不存在,请说明理由.
18.(本小题满分15分)
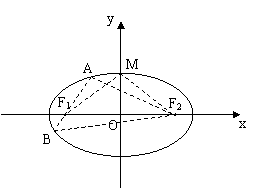
如图,椭圆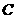 的中心在原点,焦点在
的中心在原点,焦点在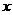 轴上,
轴上,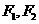 分别是椭圆
分别是椭圆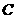 的左、右焦点,
的左、右焦点,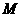 是椭圆短轴的一个端点,过
是椭圆短轴的一个端点,过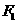 的直线
的直线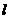 与椭圆交于
与椭圆交于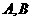 两点,
两点,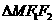 的面积为
的面积为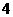 ,
, 的周长为
的周长为 .
.
(1)求椭圆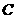 的方程;
的方程;
 (2)设点
(2)设点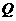 的坐标为
的坐标为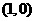 ,是否存在椭圆上的点
,是否存在椭圆上的点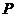 及以
及以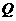 为圆心的一个圆,使得该圆与直线
为圆心的一个圆,使得该圆与直线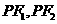 都相切,如存在,求出
都相切,如存在,求出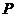 点坐标及圆的方程,如不存在,请说明理由.
点坐标及圆的方程,如不存在,请说明理由.
17.(本小题满分15分)
某企业有两个生产车间分别在A,B两个位置,A车间有100名员工,B车间有400名员工,现要在公路AC上找一点D,修一条公路BD,并在D处建一个食堂,使得所有员工均在此食堂用餐,已知A,B,C中任意两点间的距离均有1 km,设∠BDC=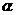 ,所有员工从车间到食堂步行的总路程为S.
,所有员工从车间到食堂步行的总路程为S.
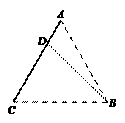 (1)写出S关于
(1)写出S关于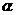 的函数表达式,并指出
的函数表达式,并指出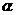 的取值范围;
的取值范围;
(2)问食堂D建在距离A多远时,可使总路程S最少?
16.(本小题满分14分)
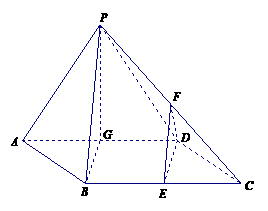 如图,四棱锥P-ABCD中,底面ABCD为菱形,且
如图,四棱锥P-ABCD中,底面ABCD为菱形,且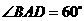 ,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
,侧面PAD是正三角形,其所在的平面垂直于底面ABCD,点G为AD的中点.
(1)求证:BG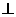 面PAD;
面PAD;
(2)E是BC的中点,在PC上求一点F,使得PG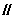 面DEF.
面DEF.
15、(本小题满分14分)
设已知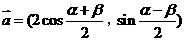 ,
,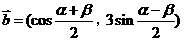 ,其中
,其中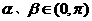 .
.
(1)若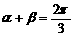 ,且
,且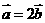 ,求
,求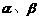 的值;
的值;
(2)若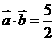 ,求
,求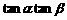 的值.
的值.
14.如果对于函数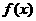 定义域内任意的两个自变量的值
定义域内任意的两个自变量的值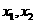 ,当
,当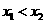 时,都有
时,都有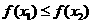 ,且存在两个不相等的自变量值
,且存在两个不相等的自变量值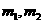 ,使得
,使得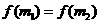 ,就称
,就称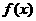 为定义域上的不严格的增函数.已知函数
为定义域上的不严格的增函数.已知函数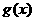 的定义域、值域分别为
的定义域、值域分别为 、
、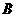 ,
,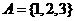 ,
,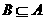 , 且
, 且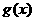 为定义域
为定义域 上的不严格的增函数,那么这样的
上的不严格的增函数,那么这样的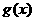 共有____________个.
共有____________个.
13.若对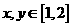 且
且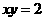 总有不等式
总有不等式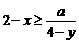 成立,则实数a的取值范围是__________.
成立,则实数a的取值范围是__________.
12.设 为坐标原点,给定一个定点
为坐标原点,给定一个定点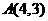 , 而点
, 而点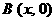 在
在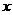 正半轴上移动,
正半轴上移动,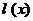 表示
表示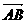 的长,则△
的长,则△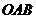 中两边长的比值
中两边长的比值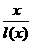 的最大值为
.
的最大值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com