
题目列表(包括答案和解析)
4.(选修4-4:不等式选讲)
设a,b,c均为正实数.
(1)若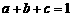 ,求
,求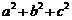 的最小值;
的最小值;
(2)求证: .
.
3.(选修4-4:坐标系与参数方程)
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若直线l
的极坐标方程为 .
.
(1)把直线l的极坐标方程化为直角坐标方程;
(2)已知P为椭圆 上一点,求P到直线l的距离的最值.
上一点,求P到直线l的距离的最值.
2.(选修4-2:矩阵与变换)
已知二阶矩阵A有特征值 及对应的一个特征向量
及对应的一个特征向量 和特征值
和特征值 及对应
及对应
的一个特征向量 ,试求矩阵A及其逆矩阵
,试求矩阵A及其逆矩阵 .
.
记分,每小题10分,共20分,请在答题卡指定区域内作答,解答应写出文字说明,证明步骤或演算步骤.
1.(选修4-1:几何证明选讲)
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过
N点的切线交CA的延长线于P.
(1)求证: ;
;
(2)若⊙O的半径为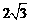 ,OA=
,OA=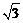 OM,求MN的长.
OM,求MN的长.

20.(本小题满分16分)
已知直线 为曲线
为曲线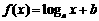 在点
在点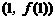 处的一条切线.
处的一条切线.
(1)求a,b的值;
(2)若函数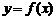 的图象
的图象 与函数
与函数 (n>0)的图象
(n>0)的图象 交于
交于 ,
,
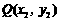 两点,其中
两点,其中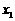 <
< ,过PQ的中点R作
,过PQ的中点R作 轴的垂线分别交
轴的垂线分别交 ,
, 于点M、N,
于点M、N,
设C1在点M处的切线的斜率为 ,C2在点N处的切线的斜率为
,C2在点N处的切线的斜率为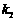 ,求证:
,求证: <
<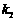 .
.
选做题部分
(时间30分钟,满分40分)
19.(本小题满分16分)
设函数 (a、b、c
(a、b、c ).
).
(1)已知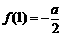 .
.
① 若 <1的解集为
<1的解集为 ,求
,求 的表达式;
的表达式;
② 若a>0,求证:函数 在区间
在区间 内至少有一个零点;
内至少有一个零点;
(2)已知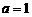 ,若
,若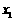 ,
,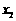 是函数
是函数 的两个零点,且
的两个零点,且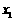 ,
,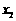
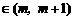 ,其中
,其中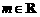 ,
,
求 的最大值.
的最大值.
18.(本小题满分16分)
根据如图所示的流程图,将输出的x值依次记为
 ;输出的y值依次记为
;输出的y值依次记为
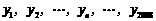 ,
,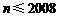 ,且
,且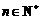 .
.
(1)求数列 的通项公式
的通项公式 ;
;
(2)设 ,
, 为
为 的前n项和,求
的前n项和,求 ;
;
(3)对于(2)中的 ,记
,记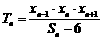 ,若对于
,若对于
一切正整数n≥2,总有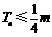 成立,求实数
成立,求实数 的取
的取
值范围.
17.(本小题满分14分)
在正方体 中,已知E、F、G分别是棱AB、AD、
中,已知E、F、G分别是棱AB、AD、 的中点.
的中点.
(1)求证:BG//平面 ;
;
(2)若P为棱 上一点,求当
上一点,求当 等于多少时,平面
等于多少时,平面 平面
平面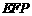 ?
?

16.(本小题满分14分)
某城市的夏季室外温度y(℃)的波动近似地按照规则
 ,
,
其中t(h)是从某日0点开始计算的时间,且t≤24.
(1)若在t0 h(t0≤6)时的该城市室外温度为19℃,求在t0+8 h时的城市室外温度;
(2)某名运动员要在这个时候到该城市参加一项比赛,计划在比赛当天的10时抵达,
且于当天16时离去,而该运动员一旦到室外温度超过36℃的地方就会影响正常发挥,
试问该运动员会不会因为气温影响而不能正常发挥?
说明,证明步骤或演算步骤.
15.(本小题满分14分)
已知圆C在x轴上的截距为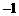 和3,在y轴上的一个截距为1.
和3,在y轴上的一个截距为1.
(1)求圆C的标准方程;
(2)若过点 的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.
的直线l被圆C截得的弦AB的长为4,求直线l的倾斜角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com