14．如图所示的流程图，根据最后输出的变量S具有的数值，则S的末位数字是__________．

解析：事实上S具有的数值为2008²⁰⁰⁹，根据题目要求只需考虑8ⁿ的尾数变化即可．

首先来观察8ⁿ的末位数字的变化规律.

8ⁿ的末位数字的变化是以4为周期的规律循环出现．

2009被4除余数为1，所以2008²⁰⁰⁹的末位数字为8.

答案：8

13．已知α是第二象限的角，且sin(π+α)＝－，则tan2α的值为__________．

解析：由sin(π+α)＝－，得sinα＝，∵α是第二象限的角，∴cosα＝－，从而得tanα＝－，

∴tan2α＝＝＝－.

答案：－

12．若函数y＝f(x)(x∈R)满足f(x+2)＝f(x)，且x∈(－1,1]时，f(x)＝1－x²，函数g(x)＝，则函数h(x)＝f(x)－g(x)在区间[－5,10]内零点的个数为(　)

A．12　 B．14　 C．13　 D．8

解析：如图，当x∈[0,5]时，结合图象知f(x)与g(x)共有5个交点，共在区间[－5,0]上共有5个交点；当x∈(0,10]时结合图象知共有9个交点．故函数h(x)＝f(x)－g(x)在区间[－5,10]上共有14个零点．

答案：B

11．已知P是直线l：3x－4y+11＝0上的动点，PA、PB是圆x²+y²－2x－2y+1＝0的两条切线，C是圆心，那么四边形PACB面积的最小值是(　)

A.　 B．2　 C.　 D．2

解析：把圆的方程化为标准方程为(x－1)²+(y－1)²＝1，则可知直线与圆相离．如图，S_{四边形PACB}＝S_△PAC+S_△PBC，

而S_△PAC＝|PA|·|CA|＝|PA|，

S_△PBC＝|PB|·|CB|＝|PB|，

又|PA|＝，|PB|＝，

∴当|PC|取最小值时，|PA|＝|PB|取最小值，即S_△PAC＝S_△PBC取最小值，此时，CP⊥l，|CP|＝＝2，则S_△PAC＝S_△PBC＝×＝，即四边形PACB面积的最小值是.

答案：C

10．已知变量x、y满足约束条件，则f(x，y)＝的取值范围是(　)

A．(，)　 B．(，+∞)

C．[，]　 D．(－∞，)

解析：

画出约束条件所表示的可行域如图中阴影部分所示，则f(x，y)＝＝，令＝k，则f(x，y)＝g(k)＝＝2－.

而k＝表示可行域内的点P(x，y)与坐标原点O的连线的斜率，观察图形可知，k_OA≤k≤k_OB，而k_OA＝＝，k_OB＝＝3，∴≤k≤3，即≤f(x，y)≤.

答案：C

9．给出如下几个结论：

①命题“∃x∈R，sinx+cosx＝2”的否定是“∃x∈R，sinx+cosx≠2”；

②命题“∀x∈R，sinx+≥2”的否定是“∃x∈R，sinx+＜2”；

③对于∀x∈(0，)，tanx+≥2；

④∃x∈R，使sinx+cosx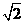＝。其中正确的为(　　　　 )

A．③ 　　　　　　B．③④

C．②③④ 　　　　D．①②③④

答案：C

8．某电视台举行大型文艺晚会，晚会演出时，为了达到更好的演唱效果，演出团从8名歌唱演员中选派4名在舞台上站成一排伴唱，其中甲、乙2人中有且仅有1人参加，则在舞台上伴唱队列的不同排列方法共有(　)

A．480种 　B．540种　 C．840种　 D．960种

解析：先从甲、乙2人中选出1人，有C种方法，再从其他6人中选出3人，有C种方法，最后让选出的4人在舞台上站成一排，有A种排法．于是，在舞台上伴唱队列的不同排列方法共有C·C·A＝960(种)．

答案：D

7．已知两单位向量a，b的夹角为60°，则两向量p＝2a+b与q＝-3a+2b的夹角为(　　 )

A．60° B．120° C．30° D．150°

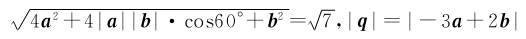
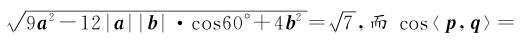
答案：B

6．已知两条不重合的直线m、n，两个互不重合的平面α、β，给出下列命题：

①若m⊥α，n⊥β，且m⊥n，则α⊥β；

②若m∥α，n∥β，且m∥n，则α∥β；

③若m⊥α，n∥β，则m⊥n，则α⊥β；

④若m⊥α，n∥β，且m∥n，则α∥β.

其中正确命题的个数为(　)

A．0　 B．1　 C．2　 D．3

解析：命题①是正确的；命题②不正确，很容易找到反例；命题③也不正确，可以构造出α∥β的情形；命题④也不正确，可以构造出α⊥β的情形．

答案：B

5．若等比数列{a_n}的前n项和为S_n＝3^2n－1+a，则常数a的值等于(　)

A．－　 B．－1　 C.　 D．3

解析：由S_n＝3^2n－1+a知，当n≥2时，a_n＝S_n－S_n－1＝3^2n－1－3^2n－3＝8×3^2n－3.

当n＝1时，a₁＝S₁＝3+a.

∵数列{a_n}是等比数列，∴3+a＝8×3^2×1－3＝，∴a＝－.

答案：A