24．(本小题10分)选修4－5：不等式选讲

已知2x+y＝1，x＞0，y＞0，求的最小值．

解析：∵2x+y＝1，x＞0，y＞0，

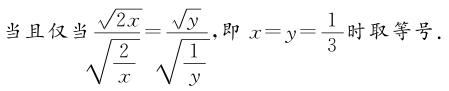
23．(本小题10分)选修4－4：坐标系与参数方程

求直线l：(t为参数)被圆C：(α为参数)截得弦长．

解析：将直线l的方程(t为参数)化为普通方程为：x+y＝2，

将圆C的方程(α为参数)化为普通方程为：x²+y²＝9，

则圆心到直线l的距离d＝＝，

∴所求弦长为2＝2＝2.

22．(本小题10分)选修4－1：几何证明选讲

如图，△ABC内接于⊙O，AB＝AC，直线MN切⊙O于点C，BE∥MN交AC于点E.若AB＝6，BC＝4，求AE的长．

解析：∵∠BCM＝∠A，BE∥MN，∴∠BCM＝∠EBC，∠A＝∠EBC.又∠ACB是公共角，∴ΔABC∽ΔBEC，∴＝.

∵AB＝AC＝6，BC＝4，∴EC＝＝＝，

∴AE＝AC－EC＝.

21．(本小题14分)已知离心率为的椭圆C：+＝1(a＞b＞0)过点M(，1)，O为坐标原点．

(1)求椭圆C的方程；

(2)已知直线l与椭圆C交于不同的两点A、B，若直线l是圆O：x²+y²＝的一条切线，试证明∠AOB＝.它的逆命题成立吗？若成立，请给出证明；否则，请说明理由．

解析：(1)因为椭圆C：+＝1(a＞b＞0)过点M(，1)，且离心率为，

所以，解得，

故椭圆C的方程为+＝1.

(2)若直线l的斜率存在，则设直线l的方程为y＝kx+m，直线l与椭圆C交于不同的两点A(x₁，y₁)，B(x₂，y₂)，

由直线l与圆O相切得r＝，即r²＝＝.

联立方程组，得x²+2(kx+m)²＝8，

即(1+2k²)x²+4kmx+2m²－8＝0，

则Δ＝16k²m²－4(1+2k²)(2m²－8)＝8(8k²－m²+4)＞0，即8k²－m²+4＞0.由方程根与系数的关系得：，

从而y₁y₂＝(kx₁+m)(kx₂+m)＝k²x₁x₂+km(x₁+x₂)+m²＝－+m²＝.要证∠AOB＝，即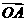⊥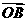，只需证x₁x₂+y₁y₂＝0，即证+＝0，即证3m²－8k²－8＝0，而＝，所以3m²－8k²－8＝0成立．即∠AOB＝.

而当直线l的斜率不存在时，直线l为x＝±，此时直线l与椭圆+＝1的两个交点为(，±)或(－，±)，满足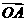⊥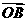.综上，有∠AOB＝.

逆命题：已知直线l与椭圆C交于不同的两点A、B，若∠AOB＝，则直线l是圆O：x²+y²＝的一条切线．结论成立．

证明：当直线l的斜率存在时，设直线l：y＝kx+m，直线l与椭圆C：+＝1的两个交点为A(x₁，y₁)，B(x₂，y₂)，联立方程组，得x²+2(kx+m)²＝8，即(1+2k²)x²+4kmx+2m²－8＝0，

则Δ＝16k²m²－4(1+2k²)(2m²－8)＝8(8k²－m²+4)＞0，即8k²－m²+4＞0，由方程根与系数的关系得：

，

则y₁y₂＝(kx₁+m)(kx₂+m)＝k²x₁x₂+km(x₁+x₂)+m²＝－+m²＝.由∠AOB＝知，⊥，即x₁x₂+y₁y₂＝0，即+＝0，所以3m²－8k²－8＝0.因为圆心到直线l的距离d＝，则d²＝＝＝，而r²＝，此时直线y＝kx+m与圆O相切．

当直线l的斜率不存在时，由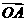⊥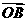可以计算得到直线l与椭圆+＝1的两个交点为(，±)或

(－，±)，此时直线l为x＝±.满足圆心到直线的距离等于半径，即直线与圆相切．

综上，其逆命题成立．

20．(本小题14分)(2009·太原模拟)设等比数列{a_n}的前n项和为S_n，首项a₁＝1，公比q＝f(λ)＝(λ≠－1,0)．

(1)证明：S_n＝(1+λ)－λa_n；

(2)若数列{b_n}满足b₁＝，b_n＝f(b_n－1)(n≥2，n∈N^*)，求数列{b_n}的通项公式；

(3)在(2)的条件下，若λ＝1，记C_n＝a_n(－1)，数列{C_n}的前n项和为T_n，求证：当n≥2时，2≤T_n＜4.

解析：(1)由题意得S_n＝＝＝(1+λ)(1－qⁿ)＝(1+λ)－(1+λ)＝(1+λ)－λ·＝(1+λ)－λa_n.

∴S_n＝(1+λ)－λa_n.

(2)∵f(λ)＝，∴b_n＝⇒＝+1，

∴{}是首项为＝2，公差为1的等差数列，

∴＝2+(n－1)＝n+1，∴b_n＝.

(3)λ＝1时，a_n＝()^n－1，

∴C_n＝a_n(－1)＝()^n－1n，

∴T_n＝1+2×()+3×()²+…+n×()^n－1，①

T_n＝+2×()²+3×()³+…+n×()ⁿ，②

①－②得：T_n＝1+()+()²+()³+…+()^n－1－n()ⁿ＝2[1－()ⁿ]－n()ⁿ，

∴T_n＝4[1－()ⁿ]－2n()ⁿ＝4－()^n－2－n()^n－1＜4，设f(n)＝T_n，则易知函数f(n)单调递增，故当n≥2时，T_n≥T₂＝2.故当n≥2时，2≤T_n＜4.

19．(本小题12分)如图，在四棱锥P－ABCD中，底面ABCD为菱形，PA⊥平面ABCD，∠ABC＝60°，E、F分别是BC，PC的中点．

(1)证明：AE⊥PD；

(2)若H为PD上的动点，EH与平面PAD所成最大角的正切值为，求二面角E－AF－C的余弦值．

解析：(1)由四边形ABCD为菱形，∠ABC＝60°，可得△ABC为正三角形．

因为E为BC的中点，所以AE⊥BC.

又BC∥AD，所以AE⊥AD.

因为PA⊥平面ABCD，AE⊂平面ABCD，

所以PA⊥AE.

而PA⊂平面PAD，AD⊂面PAD且PA∩AD＝A，所以AE⊥平面PAD.又PD⊂面PAD，所以AE⊥PD.

(2)设AB＝2，H为PD上任意一点，连接AH，如图．

由(1)知AE⊥平面PAD，则∠EHA为EH与平面PAD所成的角．

在Rt△EAH中，AE＝，所以当AH最短时，∠EHA最大，即当AH⊥PD时，∠EHA最大．此时tan∠EHA＝＝＝，因此AH＝.又AD＝2，所以∠ADH＝45°，所以PA＝2.

解法一　因为PA⊥平面ABCD，PA⊂平面PAC，所以平面PAC⊥平面ABCD.

过E作EO⊥AC于O，则EO⊥平面PAC，过O作OS⊥AF于S，连接ES，则∠ESO为二面角E－AF－C的平面角，在Rt△AOE中，EO＝AE·sin30°＝，AO＝AE·cos30°＝，又F是PC的中点，则AF⊥PC，∠FAO＝45°.则在Rt△ASO中，SO＝AO·sin45°＝，又SE＝＝ ＝，在Rt△ESO中，cos∠ESO＝＝＝，即所求二面角的余弦值为.

解法二　因为AE，AD，AP两两垂直，故以A为坐标原点，建立如图所示的空间直角坐标系，连接BD，因为E，F分别为BC，PC的中点，所以A(0,0,0)，B(，－1,0)，C(，1,0)，D(0,2,0)，P(0,0,2)，E(，0,0)，F(，，1)．

所以＝(，0,0)，＝(，，1)．

设平面AEF的一个法向量为m＝(x₁，y₁，z₁)，则，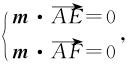

因此，取z₁＝－1，则m＝(0,2，－1)．又可知BD⊥AC，BD⊥PA，PA∩AC＝A，所以BD⊥平面AFC，故为平面AFC的一个法向量．又＝(－，3,0)，

所以cos〈m，〉＝＝＝.

因为二面角E－AF－C为锐角，所以所求二面角的余统值为.

18．(本小题12分)已知函数f(x)＝a²x³－ax²+，g(x)＝－ax+1，其中a＞0.

(1)若函数f(x)的图象与函数g(x)的图象有公共点，且在公共点处有相同的切线，试求实数a的值；

(2)在区间(0，]上至少存在一个实数x₀，使f(x₀)＞g(x₀)成立，试求实数a的取值范围．

解析：(1)设函数f(x)的图象与函数g(x)的图象的公共点为M(x₀，y₀)，则，

即.

由①得a(ax－2x₀+1)＝0，∵a＞0，且x₀≠0，

∴a＝.　③

由②得a²x－ax+ax₀－＝0.　④

把③代入④，得()²·x－·x+·x₀－＝0，化简得x－2x₀+1＝0，解得x₀＝1.

当x₀＝1时，a＝＝1，

于是，所求实数a的值为1.

(2)设F(x)＝f(x)－g(x)＝a²x³－ax²+ax－(x∈(0，])，

对F(x)求导，得F′(x)＝a²x²－2ax+a＝a²x²+a(1－2x)＞0(a＞0)，∴F(x)在(0，]上为增函数，则F(x)_max＝F()．

依题意，只需F(x)_max＞0，即a²×－a×+a×－＞0，

∴a²+6a－8＞0，

解得a＞－3+或a＜－3－(舍去)．

于是，所求实数a的取值范围是(－3+，+∞)．

17．(本小题12分)如图所示，质点P在正方形ABCD的四个顶点上按逆时针方向前进．现在投掷一个质地均匀、每个面上标有一个数字的正方体玩具，它的六个面上分别写有两个1、两个2、两个3一共六个数字．质点P从A点出发，规则如下：当正方体上底面出现的数字是1，质点P前进一步(如由A到B)；当正方体上底面出现的数字是2，质点P前进两步(如由A到C)，当正方体上底面出现的数字是3，质点P前进三步(如由A到D)．在质点P转一圈之前连续投掷，若超过一圈，则投掷终止．

(1)求质点P恰好返回到A点的概率；

(2)在质点P转一圈恰能返回到A点的所有结果中，用随机变量ξ表示点P恰能返回到A点的投掷次数，求ξ的数学期望．

解析：(1)投掷一次正方体玩具，每个数字在上底面出现都是等可能的，其概率为P₁＝＝.

只投掷一次不可能返回到A点；若投掷两次质点P就恰好能返回到A点，则上底面出现的两个数字应依次为：(1,3)、(3,1)、(2,2)三种结果，其概率为P₂＝()²×3＝；

若投掷三次质点P恰能返回到A点，则上底面出现的三个数字应依次为：(1,1,2)、(1,2,1)、(2,1,1)三种结果，其概率为P₃＝()³×3＝；

若投掷四次质点P恰能返回到A点，则上底面出现的四个数字应依次为：(1,1,1,1)．其概率为P₄＝()⁴＝.

所以，质点P恰好返回到A点的概率为：P＝P₂+P₃+P₄＝++＝.

(2)由(1)知，质点P转一圈恰能返回到A点的所有结果共有以上问题中的7种情况，且ξ的可能取值为2,3,4，

则P(ξ＝2)＝，P(ξ＝3)＝，P(ξ＝4)＝，

所以，Eξ＝2×+3×+4×＝.

16．椭圆与双曲线有许多优美的对偶性质，如对于椭圆有如下命题：AB是椭圆+＝1(a＞b＞0)的不平行于对称轴且不过原点的弦，M为AB的中点，则k_OM·k_AB＝－.那么对于双曲线则有如下命题：AB是双曲线－＝1(a＞0，b＞0)的不平行于对称轴且不过原点的弦，M为AB的中点，则k_OM·k_AB＝__________.

解析：设A(x₁，y₁)，B(x₂，y₂)，M(x₀，y₀)，则有.

∵－＝1，－＝1.

两式相减得＝，

即＝，

即＝，即k_OM·k_AB＝.

答案：

15．若f(x)＝|2x－1|－|x+1|，则满足f(x)＜2的x的取值范围为__________．

解析：①当x＜－1时，不等式f(x)＜2可转化为－(2x－1)－[－(x+1)]＜2，得x＞0，此时无解；

②当－1≤x≤时，不等式f(x)＜2可转化为－(2x－1)－(x+1)＜2，得x＞－，此时，不等式的解集为：－＜x≤；

③当x＞时，不等式f(x)＜2可转化为2x－1－(x+1)＜2，得x＜4，此时，不等式的解集为：＜x＜4.

由①、②、③得满足f(x)＜2的x的取值范围为{x|－＜x＜4}．

答案：{x|－＜x＜4}