
题目列表(包括答案和解析)
9.如图,正方体 的棱线长为1,线段
的棱线长为1,线段 上有两个动点E,F,且
上有两个动点E,F,且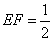 ,
, 则下列结论中错误的是
则下列结论中错误的是
(A)
(B)
(C)三棱锥 的体积为定值
的体积为定值
(D)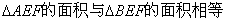
8.将函数 的图象上所有的点向左平行移动
的图象上所有的点向左平行移动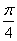 个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为
个单位长度,再把图象上各点的横坐标扩大到原来的2倍(纵坐标不变),则所得到的图象的解析式为
A. B.
B.
C. D.
D.
7.△ABC的内角A、B、C的对边分别为a、b、c. 若a、b、c成等比数列,且
(A) (B)
(B) (C)
(C) (D)
(D)
6.若 ,则目标函数
,则目标函数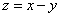 的取值范围是
的取值范围是
A.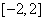 B.
B.  C.
C.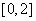 D.
D.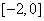
5.在平面直角坐标系中,O为坐标原点,已知点A(3,1)、B(-1,3)若点C满足 ,其中
,其中 、
、 ,且
,且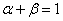 ,则点C的轨迹方程为
,则点C的轨迹方程为
A. B.
B.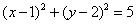
C. D.
D.
4.下列命题中,正确的命题是
A、若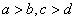 ,则
,则 B、若
B、若 ,则
,则 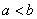
C、若 ,则
,则 D、若
D、若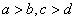 ,则
,则
3.若 ,
, ,
, ,则
,则 的值是
的值是
A.-1
B.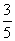 C.
C. D.
D.
2.设 是虚数单位,若
是虚数单位,若 ,则
,则 的值是
的值是
A、-1
B、1
C、 D、
D、
1.集合

A.{0,1,2} B.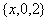 C.
C. D.
D.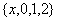
(二)选做题(14、15题,考生只能从中选做一题)
|
BD与AC交于点D,与圆交于点E,连结AE,已知ED=3,BD=6 ,
则线段AE的长= .
15. (坐标系与参数方程选做题) 已知直线
(坐标系与参数方程选做题) 已知直线 ,
,
( 为参数),若
为参数),若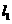 //
// ,则
,则 ;若
;若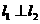 ,则
,则 .
.
16.(本小题满分12分)
已知数列 是首项为2,公比为
是首项为2,公比为 的等比数列,
的等比数列, 为
为 的前
的前 项和.
项和.
(1)求数列 的通项
的通项 及
及 ;
;
|
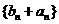 是首项为-2,公差为2的等差数列,求数列
是首项为-2,公差为2的等差数列,求数列 的通
的通
项公式及其前 项和
项和 .
.
17. (本小题满分12分)
 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.

表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面 列联表,并回答有多大的把握认为“产品的包装质量与
列联表,并回答有多大的把握认为“产品的包装质量与
两条自动包装流水线的选择有关”.
|
|
甲流水线 |
乙流水线 |
合计 |
|
合格品 |
 |
 |
|
|
不合格品 |
 |
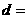 |
|
|
合 计 |
|
|
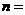 |
附:下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)

18.(本小题满分14分)
已知如图:平行四边形ABCD中, ,正方形ADEF
,正方形ADEF
所在平面与平面ABCD垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
 (2)若
(2)若 ,求四棱锥F-ABCD的体积.
,求四棱锥F-ABCD的体积.
19. (本小题满分14分)
如图,某人在塔的正东方向上的C处在与塔垂直的水
平面内沿南偏西60°的方向以每分钟100米的速度步行了
1分钟以后,在点D处望见塔的底端B在东北方向上,已
知沿途塔的仰角
 ,
, 的最大值为
的最大值为 .
.
(1)求该人沿南偏西60°的方向走到仰角 最大时,走了
最大时,走了
几分钟;
(2)求塔的高AB.
20.(本小题满分14分)
在直角坐标系 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点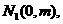
 ,
,
且 .
.
(1)求直线 与
与 交点的轨迹M的方程;
交点的轨迹M的方程;
(2)已知点G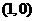 和
和 ,点P在轨迹M上运动,现以P为圆心,PG为半径作
,点P在轨迹M上运动,现以P为圆心,PG为半径作
圆P,试探究是否存在一个以点 为圆心的定圆,总与圆P内切?若存在,
为圆心的定圆,总与圆P内切?若存在,
求出该定圆的方程;若不存在,请说明理由.
21.(本小题满分14分)
已知函数  ,
, .
.
(1)当 时,求曲线
时,求曲线 在点(3,
在点(3,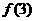 )处的切线方程;
)处的切线方程;
(2)当 时,求函数
时,求函数 在
在 上的最大值和最小值;
上的最大值和最小值;
(3)当函数 在
在 上有唯一的零点时,求实数
上有唯一的零点时,求实数 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com