
题目列表(包括答案和解析)
9.已知简谐振动
 的振幅为
的振幅为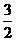 ,图象上相邻最高点与最低点之间的距离为5,且过点
,图象上相邻最高点与最低点之间的距离为5,且过点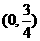 ,则该简谐振动的频率与初相分别为
,则该简谐振动的频率与初相分别为
A.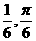 B.
B. C.
C. D.
D. 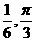
8. 的展开式中含x的正整数指数幂的项数是
的展开式中含x的正整数指数幂的项数是
A.0 B.2 C.4 D.6
7.已知 ,
, 、
、 、
、 是共起点的向量,
是共起点的向量, 、
、 不共线,
不共线, ,则
,则 、
、 、
、
 的终点共线的充分必要条件是
的终点共线的充分必要条件是
A. B.
B. C.
C. D.
D.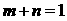
6.已知各项均不为零的数列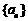 ,定义向量
,定义向量 ,
, ,
, . 下列命题中真命题是
. 下列命题中真命题是
A. 若 总有
总有 成立,则数列
成立,则数列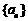 是等差数列
是等差数列
B. 若 总有
总有 成立,则数列
成立,则数列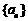 是等比数列
是等比数列
C. 若 总有
总有 成立,则数列
成立,则数列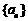 是等差数列
是等差数列
D. 若 总有
总有 成立,则数列
成立,则数列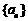 是等比数列
是等比数列
5.设 是函数
是函数 的导函数,将
的导函数,将 和
和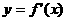 的图象画在同一个直角坐标系中,不可能正确的是
的图象画在同一个直角坐标系中,不可能正确的是

4. 如图,矩形
如图,矩形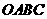 内的阴影部分是由曲线
内的阴影部分是由曲线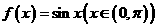 及直线
及直线 与
与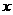 轴围成,向矩形
轴围成,向矩形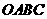 内随机投掷一点,若落在阴影部分的概率为
内随机投掷一点,若落在阴影部分的概率为 ,则
,则 的值是
的值是
A . B.
B. C
.
C
. D.
D. 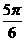
3.如图,网格纸的小正方形的边长是1,在其上用粗线画,出了某多面体的三视图,则这个多面体最长的一条棱的长为
A.  B.
B.
 C. 4
D.
C. 4
D. 
2.已知条件 ,条件
,条件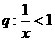 ,则
,则 是
是 成立的
成立的
A.充分不必要条件 B.必要不充分条件
 C.充要条件 D.既非充分也非必要条件
C.充要条件 D.既非充分也非必要条件
中,有且只有一项是符合题目要求的,请将正确答案填在答题卷的答题卡内)
1.已知集合 ,则
,则 等于
等于
A.(1,2) B.
[0,2] C. D. [1,2]
D. [1,2]
(15)(本小题共13分)
已知函数 ,且
,且 .
.
(Ⅰ)求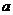 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 的值域.
的值域.
(16)(本小题共13分)
某单位在2011新年联欢会上举行一个抽奖活动:甲箱中装有3个红球,2个黑球,乙箱中装有2个红球4个黑球,参加活动者从这两个箱子中分别摸出1个球,如果摸到的都是红球则获奖.
(Ⅰ)求每个活动参加者获奖的概率;
(Ⅱ)某办公室共有5人,每人抽奖1次,求这5人中至少有3人获奖的概率.
(17)(本小题共14分)
如图,在四棱柱 中,底面
中,底面 是正方形,侧棱与底面垂直,点
是正方形,侧棱与底面垂直,点 是正方形
是正方形 对角线的交点,
对角线的交点, ,点
,点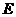 ,
, 分别在
分别在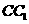 和
和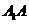 上,且
上,且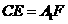 .
.
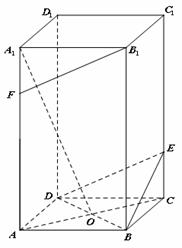 (Ⅰ)求证:
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)若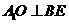 ,求
,求 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角 的余弦值.
的余弦值.
(18)(本小题共13分)
已知函数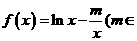 R).
R).
(Ⅰ)求函数 的定义域,并讨论函数
的定义域,并讨论函数 的单调性;
的单调性;
(Ⅱ)问是否存在实数 ,使得函数
,使得函数 在区间
在区间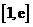 上取得最小值3?请说明理由.
上取得最小值3?请说明理由.
(19)(本小题共14分)
已知椭圆的的右顶点为A,离心率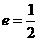 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)证明以线段 为直径的圆经过焦点
为直径的圆经过焦点 .
.
(20)(本小题共13分)
对数列 ,规定
,规定 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中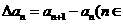 N*).对正整数k,规定
N*).对正整数k,规定 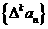 为
为 的k阶差分数列,其中
的k阶差分数列,其中
 .
.
(Ⅰ)若数列 的首项
的首项 ,且满足
,且满足 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)对(Ⅰ)中的数列 ,若数列
,若数列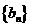 是等差数列,使得
是等差数列,使得

对一切正整数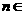 N*都成立,求
N*都成立,求 ;
;
(Ⅲ) 在(Ⅱ)的条件下,令 设
设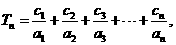 若
若 成立,求最小正整数
成立,求最小正整数 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com