
题目列表(包括答案和解析)
5.若 ,则
,则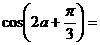
A.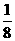 B.
B. C.
C. 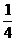 D.
D. 
|
 ,若
,若 ,则
,则 的值等于
的值等于
A.2 B.3 C.6 D.8
4.右图是统计高三年级1000名同学某次数学考试成绩的程序框图,若输出的结果是720,则这次考试数学分数不低于90分的同学的频率是
A.0.28 B.0.38 C.0.72 D.0.62
3.已知圆锥的母线长为2,母线与底面所成的角为 ,则该圆锥的表面积等于
,则该圆锥的表面积等于
A. B.
B. 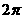 C.
C.  D.
D.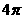
2.圆心在 轴上,半径为1,且过点(1,2)的圆的方程是
轴上,半径为1,且过点(1,2)的圆的方程是
 A.
A.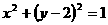 B.
B.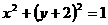
C. D.
D.
1. =
=
A.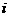 B.
B. C.
C. D.
D.
22.[2010年高考天津卷、09年浙江省高考样卷改编](本题满分15分)
设函数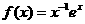 的定义域为(0,
的定义域为(0, )。
)。
(1)求函数 在
在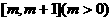 上的最小值;
上的最小值;
(2)设函数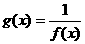 ,如果
,如果 ,且
,且 ,证明:
,证明: 。
。
(命题意图:考查函数、导数、不等式的应用及分类讨论问题。)
21.[2010年宁波一模卷改编](本题满分15分)
设椭圆C1: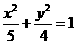 的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2:
的左、右焦点分别是F1、F2,下顶点为A,线段OA的中点为B(O为坐标原点),如图.若抛物线C2: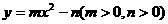
 与y轴的交点为B,且经过F1,F2点.
与y轴的交点为B,且经过F1,F2点.
(Ⅰ)求抛物线C2的方程;
(Ⅱ)设M(0, ),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求
),N为抛物线C2上的一动点,过点N作抛物线C2的切线交椭圆C1于P、Q两点,求 面积的最大值.
面积的最大值.
(命题意图:考查求曲线的轨迹方程、直线和圆锥曲线的位置关系)

20.[2009浙江省高考命题解析改编](本题满分14分)
已知数列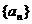 的前n项和为
的前n项和为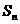 ,且满足
,且满足
(Ⅰ)求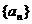 的通项公式;
的通项公式;
(Ⅱ)定义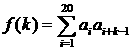 (这里规定
(这里规定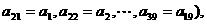
 ,求
,求 的最小值。
的最小值。
(命题意图:考查数列的性质和应用)
19.[2011浙江省高考样卷、07北京卷改编](本题满分14分)
如图,在 中,
中, ,斜边
,斜边 .
.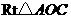 可以通过
可以通过 以直线
以直线 为轴旋转得到,且二面角
为轴旋转得到,且二面角 是直二面角.动点
是直二面角.动点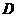 的斜边
的斜边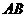 上.
上.
(I)求证:平面 平面
平面 ;
;
 (II)
(II)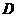 为
为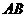 上一点,当AD=
上一点,当AD=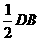 时,求异面直线
时,求异面直线 与
与 所成角的正切值;
所成角的正切值;
(III)求 与平面
与平面 所成最大角的正切值.
所成最大角的正切值.
(命题意图:考查立体几何中的线、面关系)
18.[原创](本题满分14分)在 中,角
中,角 所对的边为
所对的边为 ,已知已知
,已知已知 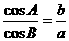 ,且
,且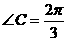 。
。
(1)求角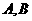 的大小;
的大小;
(2)设函数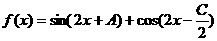 ,求函数
,求函数 在
在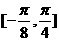 上的值域。
上的值域。
(命题意图:考查正弦定理的运用、三角函数的性质)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com