
题目列表(包括答案和解析)
17.(本小题满分12分)
在甲、乙等7个选手参加的一次演讲比赛中,采用抽签的方式随机确定每个选手的演出顺序(序号为1,2,……7),求:
(1)甲、乙两个选手的演出序号至少有一个为奇数的概率;
(2)甲、乙两选手之间的演讲选手个数 的分布列与期望.
的分布列与期望.
16.(本小题12分)
已知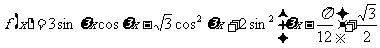 (其中
(其中 )的最小正周期为
)的最小正周期为 .
.
(1)
求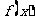 的单调递增区间;
的单调递增区间;
(2)
在 中,
中, 分别是角
分别是角 的对边,已知
的对边,已知 求角
求角 .
.
(二)选做题:第14、15题为选做题,考生只能选做一题,两题全答的,只计前一题的得分
14. (几何证明选讲选做题)如图,半径为2的⊙O中,
(几何证明选讲选做题)如图,半径为2的⊙O中, ,
, 为
为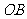 的中点,
的中点, 的延长线交⊙O于点
的延长线交⊙O于点 ,则线段
,则线段 的长为_______.
的长为_______.
15.(坐标系与参数方程选做题)曲线C的极坐标方程 ,直角坐标系中的点M的坐标为(0,2),P为曲线C上任意一点,则
,直角坐标系中的点M的坐标为(0,2),P为曲线C上任意一点,则 的最小值是
.
的最小值是
.
(一)必做题:第9、10、11、12、13题为必做题,每道试题考生都必须作答。
9. 若框图(图1)所给程序运行的结果
若框图(图1)所给程序运行的结果 ,那么
,那么
判断框中可以填入的关于 的判断条件是_ ____.
的判断条件是_ ____.
10. 已知定义域为 的函数
的函数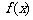 满足①
满足① ,②
,②
 ,若
,若 成等差数列,则
成等差数列,则 的值为
.
的值为
.
11.若对一切 R,复数
R,复数 的模不超过2,则实数
的模不超过2,则实数 的取值范围为
.
的取值范围为
.
12.设O点在 内部,且有
内部,且有 ,则
,则 的面积与
的面积与 的面积的比为 .
的面积的比为 .
13.记集合 ,
, ,将M中的元素按从大到小顺序排列,则第2005个数是 .
,将M中的元素按从大到小顺序排列,则第2005个数是 .
8.任意 、
、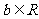 ,定义运算
,定义运算 ,则
,则 的
的
A.最小值为 B.最小值为
B.最小值为 C.最大值为
C.最大值为 D.最大值为
D.最大值为
7. 袋内有8个白球和2个红球,每次从中随机取出一个球,然后放回1个白球,则第4次恰好取完所有红球的概率为
A. 0.0324 B.0.0434 C.0.0528 D.0.0562
5. 设A1、A2为椭圆 的左右顶点,若在椭圆上存在异于A1、A2的
的左右顶点,若在椭圆上存在异于A1、A2的
点 ,使得
,使得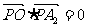 ,其中O为坐标原点,则椭圆的离心率
,其中O为坐标原点,则椭圆的离心率 的取值范围是( )
的取值范围是( )
A、 B、
B、  C、
C、 D、
D、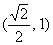
6在直三棱柱 中,
中, ,
, . 已知G与E分别为
. 已知G与E分别为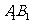 和
和 的中点,D与F分别为线段
的中点,D与F分别为线段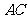 和
和 上的动点(不包括端点). 若
上的动点(不包括端点). 若 ,则线段
,则线段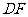 的长度的取值范围为
的长度的取值范围为
A.  B.
B. C.
C. 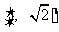 D.
D. 
4. 函数
函数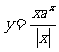
 的图象的大致形状是 ( )
的图象的大致形状是 ( )
3.下列命题不正确的是
A.如果一个平面内的一条直线垂直于另一个平面内的任意直线,则两平面垂直;
B.如果一个平面内的任一条直线都平行于另一个平面,则两平面平行;
C.如果两条不同的直线在一平面内的射影互相垂直,则这两条直线垂直;
D.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行
2.已知函数 ,若
,若 ,
,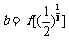 ,
, ,则( )
,则( )
A.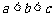 B.
B.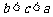 C.
C. D.
D.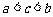
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com