
题目列表(包括答案和解析)
17.解:(1)设点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,则点
,则点 的坐标为
的坐标为 .
.
由 ,得
,得 . …………………………3分
. …………………………3分
因为点 在圆
在圆 上,则
上,则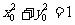 ,所以
,所以 .
.
故点 的轨迹
的轨迹 的方程为
的方程为 .
…………………………7分
.
…………………………7分
(2)因为直线 的斜率为0时,
的斜率为0时, ,故可设直线
,故可设直线 的方程为
的方程为 .
.
由 得
得 (*)……………10分
(*)……………10分
设点 ,则
,则 .
.
因为 ,则
,则 ,
,
 所以
所以 , …………………………13分
, …………………………13分
因为 ,所以
,所以 .
.
 此时(*)的判别式
此时(*)的判别式 成立,故
成立,故 的取值范围是
的取值范围是 . …………15分
. …………15分
16. 证明(1) 如图取
证明(1) 如图取 的中点为
的中点为 ,连AF,C’F, 易得AFC’F为平行四边形。
,连AF,C’F, 易得AFC’F为平行四边形。
 ,又
,又

 ………..4分
………..4分
(2)连接 ,因
,因 是菱形故有
是菱形故有

又 为正三棱柱故有
为正三棱柱故有

所以 ,而
,而
所以面 面
面 ……………9分
……………9分
(3)设B’D与BD’的交点为O ,由图得
四棱锥 与
与 的公共部分为
的公共部分为
四棱锥O-ABCD
且易得O到下底面的距离为1,

所以公共部分的体积为 。
……..14分
。
……..14分
15.解:(1)由题意,得 ……2分
……2分
于是 ,当
,当 时等号成立. …………………………4分
时等号成立. …………………………4分
所以 的最小值为
的最小值为 .
………………………… 6分
.
………………………… 6分
(2)因为 ,…………………………8分
,…………………………8分
由 ,得
,得 ,
,
所以 ,
…………………………10分
,
…………………………10分
所以
= …………………………12分
…………………………12分
当 为偶数时,
为偶数时, ;当
;当 为奇数时,
为奇数时, .…14分
.…14分
8. 500元; 9.  ; 10. ④⑤;11.
; 10. ④⑤;11.  ; 12. 0或
; 12. 0或 ;13.
;13.  ;14.
;14.  .
.
1.  ; 2. 3; 3.
; 2. 3; 3.  ;4.
;4.  ; 5.
; 5.  ;6.
;6.  ;7.
;7.  ;
;
23.(10分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对 题或答错
题或答错 题即终止其初赛的比赛:答对
题即终止其初赛的比赛:答对 题者直接进入决赛,答错
题者直接进入决赛,答错 题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为
题者则被淘汰.已知选手甲答对每个问题的概率相同,并且相互之间没有影响,答题连续两次答错的概率为 .
.
⑴求选手甲可进入决赛的概率;
⑵设选手甲在初赛中答题的个数为 ,试求
,试求 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.
必修部分答案
22、 (10分)如图6,
(10分)如图6, 是棱长为
是棱长为 的正方体,
的正方体,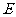 、
、 分别是棱
分别是棱 、
、 上的动点,且
上的动点,且 .
.
⑴求证: ;
;
⑵当 、
、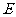 、
、 、
、 共面时,求:
共面时,求:
① 到直线
到直线 的距离;
的距离;
②面 与面
与面 所成二面角的余弦值.
所成二面角的余弦值.
2.选 :
1.选 :
21、[选做题]请从A,B,C,D四小题中选做2小题,如果多做,则按所做的前两题记分,每小题10分,共20分.解答时应写出文字说明、证明过程或演算步骤.
 A.(4-1 几何证明选讲选做题) 如图,△ABC内接于圆⊙,点D是圆⊙上异于A、B、C三点的任意一点,过D点作
A.(4-1 几何证明选讲选做题) 如图,△ABC内接于圆⊙,点D是圆⊙上异于A、B、C三点的任意一点,过D点作 ,
, ,
, ,交AB、BC、AC分别为P,Q,R.
,交AB、BC、AC分别为P,Q,R.
(1)求证:∠BDP=∠CDR;(2)求证:P,Q,R三点共线.
B.(4-2 矩阵与变换选做题)已知曲线 :
: .
.
(1)将曲线 绕坐标原点顺时针旋转
绕坐标原点顺时针旋转 后,求得到的曲线
后,求得到的曲线 的方程;
的方程;
(2)求曲线 的焦点坐标和渐近线方程.
的焦点坐标和渐近线方程.
C.(4-4 坐标系与参数方程选做题)过点 作倾斜角为
作倾斜角为 的直线
的直线 与曲线
与曲线 交于点
交于点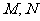 .⑴若点
.⑴若点 恰为弦
恰为弦 的中点,求直线
的中点,求直线 的方程; ⑵求
的方程; ⑵求 的最小值及相应的
的最小值及相应的 的值.
的值.
D.(4-5 不等式选讲选做题)设a、b、c均为实数,求证: +
+ +
+ ≥
≥ +
+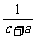 +
+ .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com