
题目列表(包括答案和解析)
5.双曲线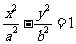 的渐近线与圆
的渐近线与圆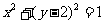 相切,则双曲线离心率为
相切,则双曲线离心率为
 (A)
(A)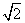 (B)
(B) (C)
(C) (D)
(D)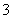
4.已知六棱锥 的底面是正六边形,
的底面是正六边形,
 平面
平面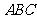 .则下列结论不正确的是
.则下列结论不正确的是
(A) 平面
平面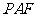
(B)
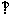 平面
平面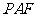
(C) 平面
平面
(D)
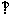 平面
平面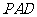
3.在 中,“
中,“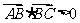 ”是“
”是“ 为钝角三角形”的
为钝角三角形”的
 (A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
2.已知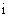 是虚数单位,则复数
是虚数单位,则复数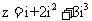 所对应的点落在
所对应的点落在
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
1.已知集合 ,
, ,且
,且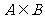 ,则
,则 等于
等于
(A) (B)
(B) (C)
(C) (D)
(D)
20. (本小题满分13分)
对于定义域分别为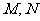 的函数
的函数 ,规定:
,规定:
函数
(1)
若函数 ,求函数
,求函数 的取值集合;
的取值集合;
(2)
若 ,设
,设 为曲线
为曲线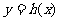 在点
在点 处切线的斜率;而
处切线的斜率;而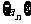 是等差数列,公差为1
是等差数列,公差为1 ,点
,点 为直线
为直线 与
与 轴的交点,点
轴的交点,点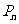 的坐标为
的坐标为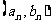 。求证:
。求证: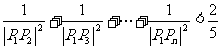 ;
;
(3)
若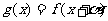 ,其中
,其中 是常数,且
是常数,且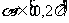 ,请问,是否存在一个定义域为
,请问,是否存在一个定义域为 的函数
的函数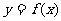 及一个
及一个 的值,使得
的值,使得 ,若存在请写出一个
,若存在请写出一个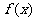 的解析式及一个
的解析式及一个 的值,若不存在请说明理由。
的值,若不存在请说明理由。
19. (本小题满分14分)
已知椭圆C的左,右焦点坐标分别为 ,离心率是
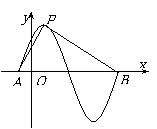
,离心率是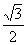 。椭圆C的左,右顶点分别记为A,B。点S是椭圆C上位于
。椭圆C的左,右顶点分别记为A,B。点S是椭圆C上位于 轴上方的动点,直线AS,BS与直线
轴上方的动点,直线AS,BS与直线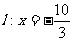 分别交于M,N两点。
分别交于M,N两点。
(1) 求椭圆C的方程;
(2) 求线段MN长度的最小值;
(3)
当线段MN的长度最小时,在椭圆C上的T满足: 的面积为
的面积为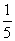 。试确定点T的个数。
。试确定点T的个数。
18. (本小题满分13分)
设函数 。
。
(1)
若函数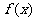 在
在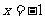 处取得极值
处取得极值 ,求
,求 的值;
的值;
(2)
若函数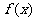 在区间
在区间 内单调递增,求
内单调递增,求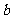 的取值范围;
的取值范围;
(3)
在(1)的条件下,若 为函数
为函数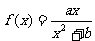 图像上任意一点,直线
图像上任意一点,直线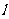 与
与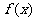 的图像切于点P,求直线
的图像切于点P,求直线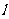 的斜率的取值范围。
的斜率的取值范围。
17. (本小题满分13分)
为振兴旅游业,某省2009年面向国内发行了总量为2000万张的优惠卡,其中向省外人士发行的是金卡,向省内人士发行的是银卡。某旅游公司组织了一个有36名游客的旅游团到该省旅游,其中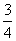 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有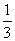 持金卡,在省内游客中有
持金卡,在省内游客中有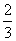 持银卡。
持银卡。
(1)在该团中随机采访3名游客,求至少有1人持金卡且恰有1人 持银卡的概率;
(2 ) 在该团的省外游客中随机采访3名游客,设其中持金卡人数为随机变量X,求X的分布列及数学期望EX。
16. (本小题满分14分)
 已知三棱锥P-ABC中,
已知三棱锥P-ABC中,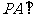 平面ABC,
平面ABC,
 ,N为AB
,N为AB
上一点,AB= 4AN, M ,D ,S分别为PB,AB,
BC的中点。
(1)求证: PA//平面CDM;
(2)求证: SN 平面CDM;
平面CDM;
(3 ) 求二面角 的大小。
的大小。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com