(1)设集合U={1,2,3,4,5},A={1,2,3},B={3,4,5}，则

(A){1，2，3，4}　　　　　　　　 (B){1，2，4，5}

(C){1，2，5}　　　　　　　　　 (D){3}

(2)若复数()是纯虚数，则的值为

(A)0　 　　　(B)2　　　　　　 　(C)0或3　 　　　(D)2或3

(3)如图，矩形长为6，宽为4，在矩形内随机地撒300颗黄豆，数得落在椭圆外的黄豆数为96颗，以此实验数据为依据可以估计出椭圆的面积约为

(A)　　　　　 　　　　　　　(B)　　　　 　　

(C)　　　 　　　　　　　　(D)

(4)如图，一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为2，那么这个几何体的体积为

(A)　　　 (B)　　　　 　　(C)　 (D)

(5)已知，且在第二象限，那么在

(A)第一象限　　　　　 　　　　　(B)第二象限

(C)第三象限 　　　　　　　　　　(D)第四象限

(6)已知点是抛物线：与直线：的一个交点，则抛物线的焦点到直线的距离是

(A)　　　 　　(B)　　 　(C)　　　 (D)

(7)△的外接圆的圆心为，半径为，若，且，则等于

(A)　　　　 (B)　　　　 (C)　　 　　(D)

(8)已知函数则函数的零点个数是

(A)　　　　 (B)　　　　 　(C)　　　　 (D)

第Ⅱ卷(共110分)

20.(本小题共13分)

已知数列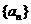的前项和为，且．数列为等比数列，且，．

(Ⅰ)求数列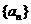，的通项公式；

(Ⅱ)若数列满足，求数列的前项和；

(Ⅲ)在(Ⅱ)的条件下，数列中是否存在三项，使得这三项成等差数列？若存在，求出此三项；若不存在，说明理由．

19.(本小题共14分)　

已知椭圆C的长轴长为，一个焦点的坐标为(1,0)．

(Ⅰ)求椭圆C的标准方程；

(Ⅱ)设直线l：y=kx与椭圆C交于A，B两点，点P为椭圆的右顶点．

(ⅰ)若直线l斜率k=1，求△ABP的面积；

(ⅱ)若直线AP，BP的斜率分别为，，求证：为定值．

(实际上，P是不同于A，B的任一点，结论都成立．)

18.(本小题共14分)

已知函数．

(Ⅰ)当时函数取得极小值，求a的值；

(Ⅱ)求函数的单调区间．

17.(本小题共13分)

某校从高一年级学生中随机抽取60名学生，将其期中考试的数学成绩(均为整数)分成六段：，，…，后得到如下频率分布直方图．

(Ⅰ)求分数在内的频率；

(Ⅱ)根据频率分布直方图，估计该校高一年级学生期中

考试数学成绩的平均分；

(Ⅲ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数不低于90分的概率．

16.(本小题共13分)

已知梯形ABCD中，，，，G，E，F分别是AD，BC，CD的中点，且，沿CG将△CDG翻折到△．

(Ⅰ)求证：EF//平面；

(Ⅱ)求证：平面⊥平面．

本题重点考查的是翻折问题。在翻折的过程中，哪些是不变的，哪些是改变的学生必须非常清楚。

15.(本小题共13分)

已知函数．

(Ⅰ)求的值；

(Ⅱ)若，求函数的最小值及取得最小值时的x值．

三角函数部分虽然已经考过几次，但二次函数型仍然没有考过，请老师们在复练时一定要练习到。

14．如图所示，已知正方形ABCD的边长为1，以A为圆心，AD长为半径画弧，交BA的延长线于P₁，然后以B为圆心，BP₁长为半径画弧，交CB的延长线于P₂，再以C为圆心，CP₂长为半径画弧，交DC的延长线于P₃，再以D为圆心，DP₃长为半径画弧，交AD的延长线于P₄，再以A为圆心，AP₄长为半径画弧，…，如此继续下去，画出的第8道弧的半径是___，画出第n道弧时，这n道弧的弧长之和为___．

本题的关键是读懂题，读懂了就非常简单。

13．一个几何体的三视图如图所示，则该几何体的体积是 　　．

12．已知签字笔2元一只，练习本1元一本．某学生欲购买的签字笔不少于3只，练习本不少于5本，但买签字笔和练习本的总数量不超过10，则支出的钱数最多是___元．

本题的关键是写对不等式组，考察学生写出不等关系，其次才是线性规划问题。