
题目列表(包括答案和解析)
21.(本小题满分14分)
已知函数
(1)若 ,解关于
,解关于 的不等式
的不等式 ;
;
(2)若对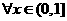 都有
都有 是常数),求
是常数),求 的取值范围.
的取值范围.
20.(本小题满分14分)
在直角坐标系 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点

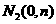 ,且
,且 .
.
(1)求直线 与
与 交点的轨迹M的方程;
交点的轨迹M的方程;
(2)已知点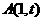 (
(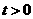 )是轨迹M上的定点,E,F是轨迹M上的两个动点,如果直线AE
)是轨迹M上的定点,E,F是轨迹M上的两个动点,如果直线AE
的斜率 与直线AF的斜率
与直线AF的斜率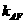 满足
满足 ,试探究直线EF的斜率是否是
,试探究直线EF的斜率是否是
定值?若是定值,求出这个定值,若不是,说明理由.
19.(本小题满分14分)
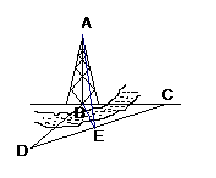
如图,某人在塔的正东方向上的C处在与塔垂直的水平面内沿南
偏西60°的方向以每小时6千米的速度步行了1分钟以后,在点D处
望见塔的底端B在东北方向上,已知沿途塔的仰角
 ,
, 的
的
最大值为 .
.
(1)求该人沿南偏西60°的方向走到仰角 最大时,走了几分钟;
最大时,走了几分钟;
(2)求塔的高AB.
18.(本小题满分14分)
 已知如图:平行四边形ABCD中,
已知如图:平行四边形ABCD中, , BD⊥CD,正方形ADEF所在平面与平面ABCD
, BD⊥CD,正方形ADEF所在平面与平面ABCD
垂直,G,H分别是DF,BE的中点.
(1)求证:GH∥平面CDE;
(2)记 ,
,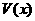 表示四棱锥F-ABCD体积,
表示四棱锥F-ABCD体积,
求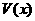 的表达式;
的表达式;
(3)当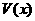 取得最大值时,求平面ECF与平面ABCD
取得最大值时,求平面ECF与平面ABCD
 所成的二面角的正弦值.
所成的二面角的正弦值.
17.(本小题满分12分)
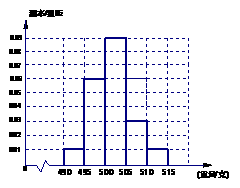
 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从乙流水线上任取5件产品,恰有3件产品为合格品的
概率;
(3)由以上统计数据完成下面 列联表,并回答有多大的把握认为“产品的包装质量与
列联表,并回答有多大的把握认为“产品的包装质量与
两条自动包装流水线的选择有关” .
|
|
甲流水线 |
乙流水线 |
合计 |
|
合格品 |
 |
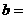 |
|
|
不合格品 |
 |
 |
|
|
合 计 |
|
|
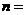 |
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
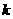 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
附:下面的临界值表供参考:
(参考公式: ,其中
,其中 )
)
证明过程和演算步骤.
16.(本小题满分12分)
|
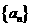 是首项为2,公比为
是首项为2,公比为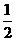 的等比数列,
的等比数列,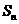 为
为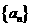 的前
的前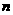 项和.
项和.
(1)求数列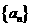 的通项
的通项 及
及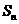 ;
;
(2)设数列 是首项为-2,第三项为2的等差数列,求数列
是首项为-2,第三项为2的等差数列,求数列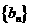 的通项公式及其
的通项公式及其
前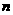 项和
项和 .
.
(二)选做题(14、15题,考生只能从中选做一题)
14.(几何证明选做题)如图所示,圆的内接三角形ABC的角平分
线BD与AC交于点D,与圆交于点E,连结AE,已知ED=3,
BD=6 ,则线段AE的长= .
15.(坐标系与参数方程选做题) 已知直线 ,
,
|

 (
( 为参数),若
为参数),若 //
// ,则
,则 ;若
;若 ,
,
则 .
.
(一)必做题(9-13题)
9. 已知 ,则使函数
,则使函数 在
在 上单调递增的所有
上单调递增的所有 值为
.
值为
.
10.已知双曲线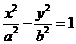 (
( >0,
>0, 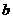 >0)的离心率为2,一个焦点与抛物线
>0)的离心率为2,一个焦点与抛物线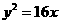 的焦点
的焦点
相同,则双曲线的焦点坐标为 ;渐近线方程为 .
11.已知 为锐角,且
为锐角,且 则
则 =
.
=
.
12.记函数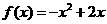 的图象与
的图象与 轴围成的区域为M,满足
轴围成的区域为M,满足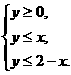 的区域为N,若向区
的区域为N,若向区
域M上随机投一点P,则点P落入区域N的概率为 .
13. 某市新年第一个月前10天监测到空气污染指数如下表(主要污染
某市新年第一个月前10天监测到空气污染指数如下表(主要污染
物为可吸入颗粒物):(第 天监测得到的数据记为
天监测得到的数据记为 )
)
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
 |
61 |
59 |
60 |
57 |
60 |
63 |
60 |
62 |
57 |
61 |
在对上述数据的分析中,一部分计算见右图所示的算法流程图
(其中 是这10个数据的平均数),则输出的
是这10个数据的平均数),则输出的 值是 ,
值是 ,
 表示的样本的数字特征是 .
表示的样本的数字特征是 .
8. 已知直线 和
和 :
: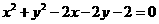 ,点A在直线
,点A在直线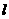 上,若直线AC与
上,若直线AC与 至少有一个公共点C,且
至少有一个公共点C,且 ,则点A的横坐标的取值范围是.
,则点A的横坐标的取值范围是.
A. B.
B. C.
C.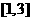 D.
D.
7. 某市汽车牌照号码可以上网自编,但规定从左到右第二个号码只能从字母B、C、D中选择,其他四个号码可以从 这十个数字中选择(数字可以重复),某车主第一个号码(从左到右)只想在数字3、5、6、8、9中选择,其他号码只想在1、3、6、9中选择,则他的车牌号码可选的所有可能情况有.
这十个数字中选择(数字可以重复),某车主第一个号码(从左到右)只想在数字3、5、6、8、9中选择,其他号码只想在1、3、6、9中选择,则他的车牌号码可选的所有可能情况有.
A.180种 B.360种 C.720种 D.960种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com