
题目列表(包括答案和解析)
1.已知 是纯虚数,
是纯虚数, 是实数(其中
是实数(其中 为虚数单位),则
为虚数单位),则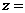
A.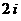 B.
B. C.
C. D.
D. 
21.(本小题满分14分)数列 中,若存在常数
中,若存在常数 ,均有
,均有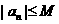 ,称数列
,称数列 是有界数列;把
是有界数列;把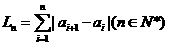 叫数列
叫数列 的前
的前 项邻差和,数列
项邻差和,数列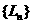 叫数列
叫数列 的邻差和数列。
的邻差和数列。
(1)若数列 满足,
满足, ,均有
,均有 恒成立,试证明:
恒成立,试证明: 是有界数列;
是有界数列;
(2)试判断公比为 的正项等比数列
的正项等比数列 的邻差和数列
的邻差和数列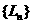 是否为有界数列,证明你的结论;
是否为有界数列,证明你的结论;
(3)已知数列 、
、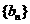 的邻差和
的邻差和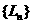 与
与 均为有界数列,试证明数列
均为有界数列,试证明数列 的邻差和数列
的邻差和数列 也是有界数列。
也是有界数列。
20、(满分14分).已知圆 与直线
与直线 相切。
相切。
(1) 求以圆O与y轴的交点为顶点,直线在x轴上的截距为半长轴长的椭圆C方程;
(2)
已知点A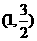 ,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线AF的斜率互为相反数;问直线的斜率是否为定值?若是求出这个定值;若不是,请说明理由.
,若直线与椭圆C有两个不同的交点E,F,且直线AE的斜率与直线AF的斜率互为相反数;问直线的斜率是否为定值?若是求出这个定值;若不是,请说明理由.
19.(本小题共14分)已知 .
.
(1)求函数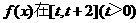 上的最小值;
上的最小值;
(2)已知 对任意
对任意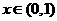 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)证明:对一切 ,都有
,都有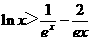 成立.
成立.
18. (本小题满分14分)如图,△ABC的外接圆⊙
(本小题满分14分)如图,△ABC的外接圆⊙ 的半径为
的半径为 ,CD
,CD ⊙
⊙ 所在的平面,BE//CD,CD=4,BC=2,且BE=1,
所在的平面,BE//CD,CD=4,BC=2,且BE=1, .
.
(1)求证:平面ADC 平面BCDE;
平面BCDE;
(2)求几何体ABCDE的体积;
(3)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为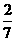 ?若存在,确定点M的位置,若不存在,请说明理由。
?若存在,确定点M的位置,若不存在,请说明理由。
17、(本小题满分12分)某公司对工厂A的一批产品进行了抽样检测。右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,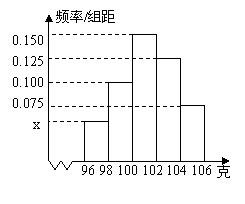 104),[104,106]。
104),[104,106]。
(1)求图中x的值;
(2)若将频率视为概率,从这批产品中有放回地随机抽取3件,求至多有2件产品的净重在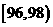 的概率;
的概率;
(3)经过考察后,该公司决定在2011年年初投资到工厂A50万元,到年底可能获利 ,也可能亏损
,也可能亏损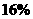 ,且这两种情况发生的概率分别为合格产品和不合格产品的概率(若产品净重在
,且这两种情况发生的概率分别为合格产品和不合格产品的概率(若产品净重在 为合格产品,其余为不合格产品)。设2011年底公司的投资总资产(本金+利润)为
为合格产品,其余为不合格产品)。设2011年底公司的投资总资产(本金+利润)为 ,求
,求 的分布列及数学期望。
的分布列及数学期望。
16.(本小题满分12分)在 中,角
中,角 、
、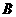 、
、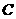 所对的边分别是
所对的边分别是 、
、 、
、 ,且
,且 (其中
(其中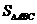 为
为 的面积)。
的面积)。
(1)求 的值;
的值;
(2)若 的面积
的面积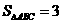 ,求
,求 的值。
的值。
15.(几何证明选讲)如图5,半径是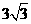 的⊙
的⊙ 中,
中, 是直径,
是直径,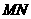 是过点
是过点 的⊙
的⊙ 的切线,
的切线, 相交于点
相交于点 ,且
,且 ,
, ,又
,又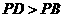 ,则线段
,则线段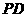 的长为
。
的长为
。
14. (坐标系与参数方程选做题)已知曲线
(坐标系与参数方程选做题)已知曲线 的极坐标方程为:
的极坐标方程为: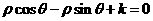 ,其中
,其中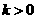 。以极点为坐标原点,极轴为
。以极点为坐标原点,极轴为 正半轴,建立平面直角坐标系,在此坐标系下,曲线
正半轴,建立平面直角坐标系,在此坐标系下,曲线 的方程为
的方程为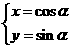 (
(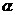 为参数)。若曲线
为参数)。若曲线 与曲线
与曲线 相切,则
相切,则 。
。
13.已知两定点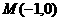 ,
, ,若直线上存在点
,若直线上存在点 ,使得
,使得 ,则该直线为“
,则该直线为“ 型直线”.给出下列直线,其中是“
型直线”.给出下列直线,其中是“ 型直线”的是
.
型直线”的是
.
①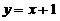 ②
② ③
③ ④
④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com