4．设函数y＝xsinx+cosx的图象上的点(x，y)处的切线斜率为k，若k＝g(x)，则函数k＝g(x)的图象大致为(　)

解析：k＝g(x)＝y′＝sinx+xcosx－sinx＝xcosx，故函数k＝g(x)为奇函数，排除A、C；又当x∈(0，)时，g(x)>0.

答案：B

3．y＝x²cosx的导数是(　)

A．y′＝2xcosx+x²sinx　 B．y′＝2xcosx－x²sinx

C．y＝2xcosx　 D．y′＝－x²sinx

解析：y′＝2xcosx－x²sinx.

答案：B

2．曲线y＝在点(－1，－1)处的切线方程为(　)

A．y＝2x+1　 　　　　　　　　　　　　 B．y＝2x－1

C．y＝－2x－3　 　　　　　　　　　　　　　　 D．y＝－2x－2

解析：∵y′＝＝，

∴k＝y′|_x＝－1＝＝2，

∴切线方程为：y+1＝2(x+1)，即y＝2x+1.

答案：A

1．已知直线y＝kx+1与曲线y＝x³+ax+b切于点(1,3)，则b的值为(　)

A．3　　　　　B．－3

C．5 　　　　　　　　　 　　　　　　 　D．－5

解析：∵y′＝3x²+a，∴k＝y′|_x＝1＝3+a.

又点(1,3)为切点，

∴解得b＝3.

答案：A

7．函数f(x)＝x²－lnx的最小值为________．

解析：得x>1，得0<x<1.

∴f(x)在x＝1时取最小值f(1)＝－ln1＝.

6．f(x)是定义在(0，+∞)上的非负可导函数，且满足xf′(x)+f(x)≤0，对任意正数a，b，若a<b，则必有(　)

A．af(b)≤bf(a)　 　　　　　　　　　　　　　　 B．bf(a)≤af(b)

C．af(a)≤f(b)　 　　　　　　　　　　　 D．bf(b)≤f(a)

解析：∵xf′(x)+f(x)≤0，

又f(x)≥0，∴xf′(x)≤－f(x)≤0，

设y＝，则y′＝≤0，

故y＝为减函数或常函数．

又a<b，∴≥，

而a，b>0，则af(b)≤bf(a)．

答案：A

5．已知f(x)＝x³－ax在[1，+∞)上是单调增函数，则a的最大值是(　)

A．0　 　　　　　　　　　　　　 B．1

C．2　 　　　　　　　　　　　　 D．3

解析：f′(x)＝3x²－a≥0在[1，+∞)上恒成立，

即：a≤3x²在[1，+∞)上恒成立，而(3x²)_min＝3×1²＝3.

∴a≤3，故a_max＝3.

答案：D

4．函数f(x)＝x³+3x²+4x－a的极值点的个数是(　)

A．2　 　　　　　　　　　　　　 B．1

C．0　 　　　　　　　　　　　　 D．由a确定

解析：f′(x)＝3x²+6x+4＝3(x+1)²+1>0，则f(x)在R上是增函数，故不存在极值点．

答案：C

3．f(x)的导函数f′(x)的图象如图所示，则函数f(x)的图象最有可能的是图中的(　)

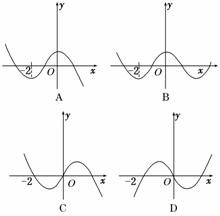
解析：∵x∈(－∞，－2)∪(0，+∞)时f′(x)<0，

∴在(－∞，－2)和(0，+∞)上f(x)是减函数，排除B、C、D.

答案：A

2．函数f(x)＝1+x－sinx在(0,2π)上是(　)

A．增函数

B．减函数

C．在(0，π)上增，在(π，2π)上减

D．在(0，π)上减，在(π，2π)上增

解析：f′(x)＝1－cosx>0，∴f(x)在(0,2π)上递增．

答案：A