6．已知函数f(x)满足：当x≥4时，f(x)＝()^x；当x＜4时，f(x)＝f(x+1)，则f(2+log₂3)＝(　)

A.　 　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　 D.

解析：∵2＜3＜4＝2²，∴1＜log₂3＜2.

∴3＜2+log₂3＜4，

∴f(2+log₂3)＝f(3+log₂3)＝f(log₂24)

＝()＝2＝2＝.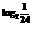

答案：A

5．设函数f(x)定义在实数集上，f(2－x)＝f(x)，且当x≥1时，f(x)＝lnx，则有(　)

A．f()<f(2)<f()　 　　　　　　　　　 B．f()<f(2)<f()

C．f()<f()<f(2)　 　　　　　　　　　 D．f(2)<f()<f()

解析：由f(2－x)＝f(x)可知f(x)关于直线x＝1对称，

当x≥1时，f(x)＝lnx，可知当x≥1时f(x)为增函数，

所以当x<1时f(x)为减函数，

因为|－1|<|－1|<|2－1|，

所以f()<f()<f(2)．

答案：C

4．函数y＝ln(1－x)的图象大致为(　)

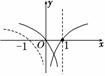解析：依题意由y＝lnx的图象关于y轴对称可得到y＝ln(－x)的图象，再将其图象向右平移1个单位即可得到y＝ln(1－x)的图象，变换过程如图．

答案：C

3．设a＝log₃2，b＝ln2，c＝5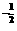，则(　)

A．a<b<c 　　 　　　　　　 B．b<c<a

C．c<a<b　 　　　　　　　　 D．c<b<a

解析：a＝log₃2＝<ln2＝b，又c＝5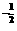＝<，a＝log₃2>log₃＝，因此c<a<b.

答案：C

2．若函数y＝f(x)是函数y＝a^x(a＞0，且a≠1)的反函数，且f(2)＝1，则f(x)＝(　)

A．log₂x　 　　　　　　　　　 B.

C．logx　 　　　　　　　　 D．2^x－2

解析：f(x)＝log_ax，∵f(2)＝1，∴log_a2＝1，∴a＝2.

∴f(x)＝log₂x.

答案：A

1．已知log₇[log₃(log₂x)]＝0，那么x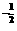 等于(　)

A.　 　　　　　　　　　 B.

C. 　　　　　 　　　 D.

解析：由条件知，log₃(log₂x)＝1，∴log₂x＝3，∴x＝8，

∴x＝.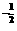

答案：C

12．已知函数f(x)＝ax²+bx+c(a＞0，b∈R，c∈R)．

(1)若函数f(x)的最小值是f(－1)＝0，且c＝1，

F(x)＝求F(2)+F(－2)的值；

(2)若a＝1，c＝0，且|f(x)|≤1在区间(0,1]上恒成立，试求b的取值范围．

解：(1)由已知c＝1，f(－1)＝a－b+c＝0，且－＝－1，解得a＝1，b＝2.

∴f(x)＝(x+1)².

∴F(x)＝

∴F(2)+F(－2)＝(2+1)²+[－(－2+1)²]＝8.

(2)由题知f(x)＝x²+bx，原命题等价于－1≤x²+bx≤1在x∈(0,1]上恒成立，即b≤－x且b≥－－x在x∈(0,1]上恒成立，

根据单调性可得－x的最小值为0，

－－x的最大值为－2，所以－2≤b≤0.

11．(2010·浏阳模拟)已知二次函数f(x)的图象过A(－1,0)、B(3,0)、C(1，－8)．

(1)求f(x)的解析式；

(2)求f(x)在x∈[0,3]上的最值；

(3)求不等式f(x)≥0的解集．

解：(1)由题意可设f(x)＝a(x+1)(x－3)，

将C(1，－8)代入得－8＝a(1+1)(1－3)，∴a＝2，

即f(x)＝2(x+1)(x－3)＝2x²－4x－6.

(2)f(x)＝2(x－1)²－8

当x∈[0,3]时，由二次函数图象知

f(x)_min＝f(1)＝－8，f(x)_max＝f(3)＝0.

(3)f(x)≥0的解集为{x|x≤－1或x≥3}．

10．已知函数f(x)＝－x^m，且f(4)＝－.

(1)求m的值；

(2)判断f(x)在(0，+∞)上的单调性，并给予证明．

解：(1)∵f(4)＝－，∴－4^m＝－.∴m＝1.

(2)f(x)＝－x在(0，+∞)上单调递减，

证明如下：

任取0<x₁<x₂，则f(x₁)－f(x₂)

＝(－x₁)－(－x₂)＝(x₂－x₁)(+1)．

∵0<x₁<x₂，∴x₂－x₁>0，+1>0.

∴f(x₁)－f(x₂)>0，∴f(x₁)>f(x₂)，

即f(x)＝－x在(0，+∞)上单调递减．

9．当x∈(1,2)时，不等式x²+mx+4<0恒成立，则m的取值范围是__________．

解析：法一：∵不等式x²+mx+4<0对x∈(1,2)恒成立，∴mx<－x²－4对x∈(1,2)恒成立，

即m<－对x∈(1,2)恒成立，令y＝x+，

则函数y＝x+在x∈(1,2)上是减函数，∴4<y<5，

∴－5<－<－4，∴m≤－5.

法二：设f(x)＝x²+mx+4，x∈(1,2)时，f(x)<0恒成立⇔⇔⇒m≤－5.

答案：(－∞，－5]