
题目列表(包括答案和解析)
6. 函数f(x)= -cosx在[0,+∞)内 ( )
-cosx在[0,+∞)内 ( )
5. 某几何体的三视图如图所示,则它的体积是( )
(A)
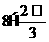
(B)
(C)8-2π
(D)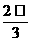
3.设函数 满足
满足 ,则
,则 的图像可能是( )
的图像可能是( )
 4.
4.  (x∈R展开式中的常数项是 ( )
(x∈R展开式中的常数项是 ( )
(A)-20 (B)-15 (C)15 (D)20
2.设抛物线的顶点在原点,准线方程为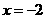 ,则抛物线的方程是 ( )
,则抛物线的方程是 ( )
(A) (B)
(B)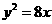 (C)
(C) 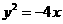 (D)
(D) 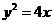
1. 设 是向量,命题“若
是向量,命题“若 ,则∣
,则∣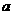 ∣= ∣
∣= ∣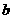 ∣”的逆命题是 ( )
∣”的逆命题是 ( )
(A)若 ,则∣
,则∣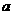 ∣
∣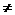 ∣
∣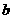 ∣
(B)若
∣
(B)若 ,则∣
,则∣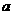 ∣
∣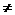 ∣
∣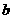 ∣
∣
(C)若∣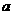 ∣
∣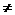 ∣
∣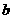 ∣,则∣
∣,则∣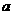 ∣
∣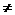 ∣
∣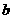 ∣ (D)若∣
∣ (D)若∣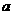 ∣=∣
∣=∣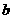 ∣,则
∣,则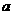 = -
= -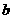
(15)(本小题共13分)
已知函数 。
。
(Ⅰ)求 的最小正周期:
的最小正周期:
(Ⅱ)求 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。
(16)(本小题共14分)
如图,在四棱锥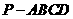 中,
中,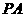
 平面
平面 ,底面
,底面 是菱形,
是菱形, .
.

(Ⅰ)求证: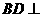 平面
平面
(Ⅱ)若 求
求 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅲ)当平面 与平面
与平面 垂直时,求
垂直时,求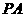 的长.
的长.
(17)本小题共13分
以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊,无法确认,在图中以X表示。
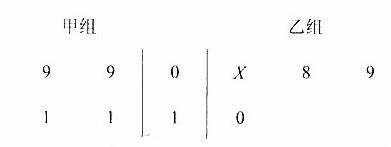
(Ⅰ)如果X=8,求乙组同学植树棵树的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵树Y的分布列和数学期望。
(注:方差 ,其中
,其中 为
为 ,
,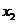 ,……
,……  的平均数)
的平均数)
(18)(本小题共13分)
已知函数 。
。
(Ⅰ)求 的单调区间;
的单调区间;
(Ⅱ)若对于任意的 ,都有
,都有 ≤
≤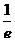 ,求
,求 的取值范围。
的取值范围。
(19)(本小题共14分)
已知椭圆 .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.
(I)求椭圆G的焦点坐标和离心率;
(II)将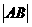 表示为m的函数,并求
表示为m的函数,并求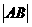 的最大值.
的最大值.
(20)(本小题共13分)
若数列 满足
满足 ,数列
,数列 为
为 数列,记
数列,记 =
= .
.
(Ⅰ)写出一个满足 ,且
,且 〉0的
〉0的 数列
数列 ;
;
(Ⅱ)若 ,n=2000,证明:E数列
,n=2000,证明:E数列 是递增数列的充要条件是
是递增数列的充要条件是 =2011;
=2011;
(Ⅲ)对任意给定的整数n(n≥2),是否存在首项为0的E数列 ,使得
,使得 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列 ;如果不存在,说明理由。
;如果不存在,说明理由。
(9)在 中。若b=5,
中。若b=5, ,tanA=2,则sinA=____________;a=_______________。
,tanA=2,则sinA=____________;a=_______________。
(10)已知向量a=(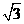 ,1),b=(0,-1),c=(k,
,1),b=(0,-1),c=(k,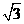 )。若a-2b与c共线,则k=___________________。
)。若a-2b与c共线,则k=___________________。
(11)在等比数列{an}中,a1= ,a4=-4,则公比q=______________;
,a4=-4,则公比q=______________; _________________。
_________________。
(12)用数字2,3组成四位数,且数字2,3至少都出现一次,这样的四位数共有__________个。(用数字作答)
(13)已知函数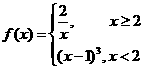 若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是_______
若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是_______
(14)曲线C是平面内与两个定点F1(-1,0)和F2(1,0)的距离的积等于常数 a2 (a >1)的点的轨迹.给出下列三个结论:
① 曲线C过坐标原点;
② 曲线C关于坐标原点对称;
③若点P在曲线C上,则△F PF
PF 的面积大于
的面积大于 a
a 。
。
 其中,所有正确结论的序号是
。
其中,所有正确结论的序号是
。
(1)已知集合P={x︱x2≤1},M={a}.若P∪M=P,则a的取值范围是
(A)(-∞, -1] (B)[1, +∞) (C)[-1,1] (D)(-∞,-1] ∪[1,+∞)
(2)复数
(A)i
(B)-i
(C) (D)
(D)
 (3)在极坐标系中,圆ρ=-2sinθ的圆心的极坐标系是
(3)在极坐标系中,圆ρ=-2sinθ的圆心的极坐标系是
(A)  (B)
(B)
 (C) (1,0)
(D)(1,
(C) (1,0)
(D)(1,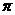 )
)
(4)执行如图所示的程序框图,输出的s值为
(A)-3
(B)-
(C)
(D)2
(5)如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G。给出下列三个结论:
1AD+AE=AB+BC+CA;
2AF·AG=AD·AE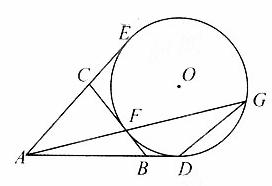
③△AFB -△ADG
其中正确结论的序号是
(A)①② (B)②③
(C)①③ (D)①②③
(6)根据统计,一名工作组装第4件某产品所用的时间(单位:分钟)为 (A,C为常数)。已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么C和A的值分别是
(A,C为常数)。已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么C和A的值分别是
(A)75,25 (B)75,16 (C)60,25 (D)60,16
(7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是

(A) 8 (B)  (C)10 (D)
(C)10 (D) 
(8)设 ,
, ,
,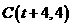 ,
, .记
.记 为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数
为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数 的值域为
的值域为
(A) (B)
(B)
(C) (D)
(D)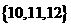
(15)(本小题共13分)
已知函数
(Ⅰ)求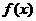 的最小正周期;
的最小正周期;
(Ⅱ)求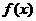 在区间
在区间 上的最大值和最小值。
上的最大值和最小值。
(16)(本小题共13分)
以下茎叶图记录了甲、乙两组各四名同学的植树棵数。乙组记录中有一个数据模糊,无法确认,在图中经X表示。

(Ⅰ)如果X=8,求乙组同学植树棵数的平均数和方差;
(Ⅱ)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率。
(注:方差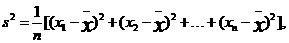 其中
其中 为
为 ,
, ,
,
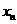 的平均数)
的平均数)
(17)(本小题共14分)
 如图,在四面体
如图,在四面体 中,
中, 点
点 分别是棱
分别是棱 的中点。
的中点。
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:四边形 为矩形;
为矩形;
(Ⅲ )是否存在点 ,到四面体
,到四面体 六条棱的中点 的距离相等?说明理由。
六条棱的中点 的距离相等?说明理由。
(18)(本小题共13分)
已知函数 。
。
(Ⅰ)求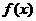 的单调区间;
的单调区间;
(Ⅱ)求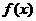 在区间
在区间 上的最小值。
上的最小值。
(19)(本小题共14分)
已知椭圆 的离心率为
的离心率为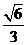 ,右焦点为
,右焦点为 。斜率为1的直线
。斜率为1的直线 与椭圆
与椭圆 交于
交于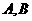 两点,以
两点,以 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为 。
。
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求 的面积。
的面积。
(20)(本小题共13分)
若数列 满足
满足
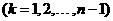 ,则称
,则称 为
为 数列。记
数列。记 。
。
(Ⅰ)写出一个 数列
数列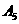 满足
满足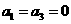 ;
;
(Ⅱ)若 ,证明:
,证明: 数列
数列 是递增数列的充要条件是
是递增数列的充要条件是 ;
;
(Ⅲ)在 的
的 数列
数列 中,求使得
中,求使得 成立的
成立的 的最小值。
的最小值。
(9)在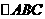 中,若
中,若 ,则
,则 .
.
(10)已知双曲线 的一条渐近线的方程为
的一条渐近线的方程为 ,则
,则 .
.
(11)已知向量 。若
。若 与
与 ,共线,则
,共线,则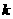 = .
= .
(12)在等比数列 中,若
中,若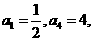 则公比
则公比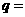 ;
;
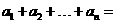 .
.

(13)已知函数 若关于 的方程
的方程 有两个不同的实
有两个不同的实
根,则实数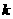 的取值范围是
.
的取值范围是
.
(14)设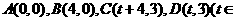 R)。记
R)。记 为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则
为平行四边形ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则 ;
;  的所有可能取值为
。
的所有可能取值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com