
题目列表(包括答案和解析)
4.在△ABC中,点P在BC上,且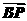 =2
=2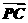 ,点Q是AC的中点,若
,点Q是AC的中点,若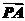 =(4,3),
=(4,3),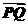 =(1,5),则
=(1,5),则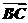 =( )
=( )
A.(-2,7) B.(-6,21)
C.(2,-7) D.(6,-21)
解析: =
=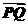 -
-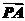 =(-3,2),∴
=(-3,2),∴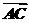 =2
=2 =(-6,4).
=(-6,4).
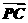 =
=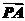 +
+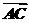 =(-2,7),∴
=(-2,7),∴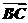 =3
=3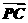 =(-6,21).
=(-6,21).
答案:B
3.已知向量a=(1,-m),b=(m2,m),则向量a+b所在的直线可能为( )
A.x轴 B.第一、三象限的角平分线
C.y轴 D.第二、四象限的角平分线
解析:a+b=(1,-m)+(m2,m)=(m2+1,0),其横坐标恒大于零,纵坐标等于零,故向量a+b所在的直线可能为x轴.
答案:A
2.已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且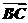 =2
=2 ,则顶点D的坐标为( )
,则顶点D的坐标为( )
A. B.
C.(3,2) D.(1,3)
解析:设D(x,y), =(x,y-2),
=(x,y-2),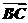 =(4,3),
=(4,3),
又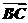 =2
=2 ,
,
∴∴即点D坐标为(2,).
答案:A
1.已知命题:“若k1a+k2b=0,则k1=k2=0”是真命题,则下面对a、b的判断正确的是( )
A.a与b一定共线 B.a与b一定不共线
C.a与b一定垂直 D.a与b中至少有一个为0
解析:由平面向量基本定理可知,当a、b不共线时,k1=k2=0.
答案:B
21.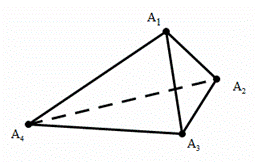 (本小题满分14分)
(本小题满分14分)
(1)如图,对于任一给定的四面体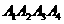 ,找出依
,找出依
次排列的四个相互平行的平面 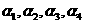 ,使
,使
得 (i=1,2,3,4),且其中每相邻两个平面间
(i=1,2,3,4),且其中每相邻两个平面间
的距离都相等;
(2)给定依次排列的四个相互平行的平面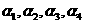 ,其中每相邻两个平面间的距离为1,若一个正四面体
,其中每相邻两个平面间的距离为1,若一个正四面体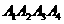 的四个顶点满足:
的四个顶点满足: (i=1,2,3,4),求该正四面体
(i=1,2,3,4),求该正四面体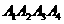 的体积.
的体积.
解:
(1)将直线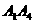 三等分,其中另两个分点依次为
三等分,其中另两个分点依次为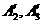 ,连接
,连接 ,作平行于
,作平行于 的平面,分别过
的平面,分别过 ,即为
,即为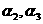 。同理,过点
。同理,过点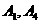 作平面
作平面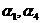 即可的出结论。
即可的出结论。
(2)现设正方体的棱长为a,若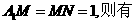 ,
,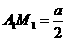 ,
,
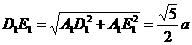 ,由于
,由于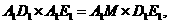
 得,
得,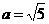 ,
,
那么,正四面体的棱长为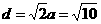 ,其体积为
,其体积为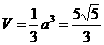 (即一个棱长为a的正方体割去四个直角三棱锥后的体积)
(即一个棱长为a的正方体割去四个直角三棱锥后的体积)
20.(本小题满分13分)
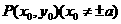 是双曲线
是双曲线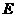 :
: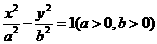 上一点,
上一点,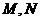 分别是双曲线
分别是双曲线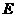 的左、右定点,直线
的左、右定点,直线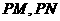 的斜率之积为
的斜率之积为 .
.
(1)求双曲线的离心率;
(2)过双曲线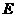 的右焦点且斜率为1的直线交双曲线于
的右焦点且斜率为1的直线交双曲线于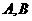 两点,
两点, 为坐标原点,
为坐标原点,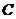 为双曲线上的一点,满足
为双曲线上的一点,满足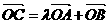 ,求
,求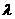 的值.
的值.
解:(1)已知双曲线E: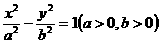 ,
,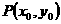 在双曲线上,M,N分别为双曲线E的左右顶点,所以
在双曲线上,M,N分别为双曲线E的左右顶点,所以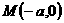 ,
,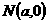 ,直线PM,PN斜率之积为
,直线PM,PN斜率之积为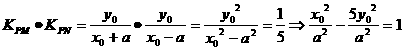
而 ,比较得
,比较得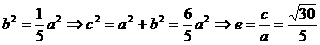
(2)设过右焦点且斜率为1的直线L: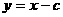 ,交双曲线E于A,B两点,则不妨设
,交双曲线E于A,B两点,则不妨设 ,又
,又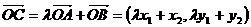 ,点C在双曲线E上:
,点C在双曲线E上:
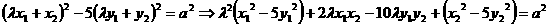 *(1)
*(1)
又 联立直线L和双曲线E方程消去y得: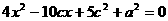
由韦达定理得: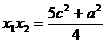 ,
, 代入(1)式得:
代入(1)式得: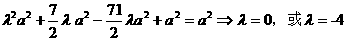
19.(本小题满分12分)
设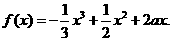
(1)若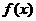 在
在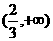 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围;
的取值范围;
(2)当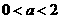 时,
时,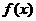 在
在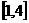 上的最小值为
上的最小值为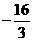 ,求
,求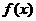 在该区间上的最大值.
在该区间上的最大值.
解:(1)已知 ,
,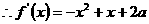 ,函数
,函数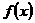 在
在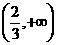 上存在单调递增区间,即导函数在
上存在单调递增区间,即导函数在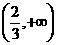 上存在函数值大于零的部分,
上存在函数值大于零的部分,
(2)已知0<a<2, 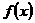 在
在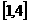 上取到最小值
上取到最小值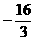
 ,而
,而 的图像开口向下,且对轴
的图像开口向下,且对轴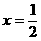 ,
,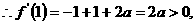
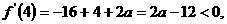
则必有一点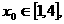 使得
使得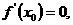 此时函数
此时函数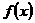 在
在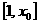 上单调递增,在
上单调递增,在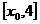 单调递减,
单调递减,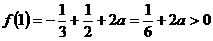 ,
,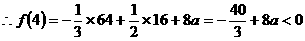
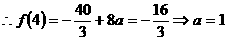
此时,由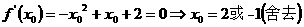 ,所以函数
,所以函数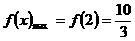
18.(本小题满分12分)
已知两个等比数列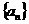 ,
,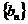 ,满足
,满足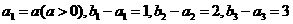 .
.
(1)若 =1,求数列
=1,求数列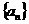 的通项公式;
的通项公式;
(2)若数列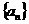 唯一,求
唯一,求 的值.
的值.
.解:(1)当a=1时,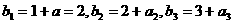 ,又
,又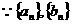 为等比数列,不妨设
为等比数列,不妨设 公比为
公比为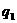 ,由等比数列性质知:
,由等比数列性质知: 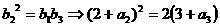 ,同时又有
,同时又有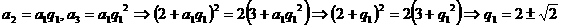 所以:
所以: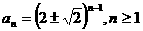
(2) 要唯一,
要唯一, 当公比
当公比 时,由
时,由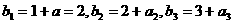 且
且
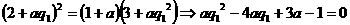 ,
,
 ,
,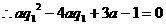 最少有一个根(有两个根时,保证仅有一个正根)
最少有一个根(有两个根时,保证仅有一个正根)
 ,此时满足条件的a有无数多个,不符合。
,此时满足条件的a有无数多个,不符合。
 当公比
当公比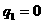 时,等比数列
时,等比数列 首项为a,其余各项均为常数0,唯一,此时由
首项为a,其余各项均为常数0,唯一,此时由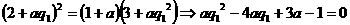 ,可推得
,可推得 符合
符合
综上: 。
。
17.(本小题满分12分)
在△ABC中,角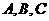 的对边分别是
的对边分别是 ,已知
,已知 .
.
(1)求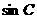 的值;
的值;
(2)若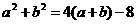 ,求边
,求边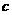 的值.
的值.
解:(1)已知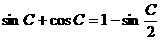
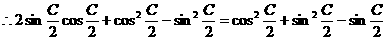
整理即有: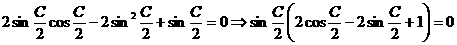
又C为 中的角,
中的角,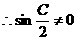
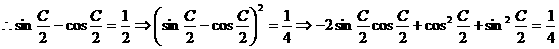
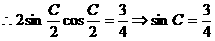
(2)

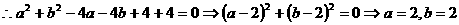
又 ,
,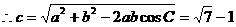
16.(本小题满分12分)
某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3500元;若4杯选对3杯,则月工资定为2800元;否则月工资定为2100元.令X表示此人选对A饮料的杯数.假设次人对A和B两种饮料没有鉴别能力.
(1)求X的分布列;
(2)求此员工月工资的期望.
解答:(1)选对A饮料的杯数分别为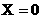 ,
,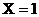 ,
,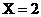 ,
,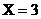 ,
,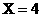 ,
,
其概率分布分别为: 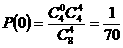 ,
,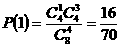 ,
,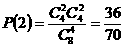 ,
,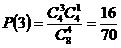 ,
,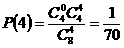 。
。
(2)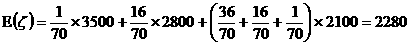 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com