
题目列表(包括答案和解析)
5.(广东省北江中学2009届高三上学期12月月考)
已知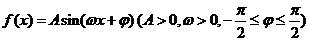 的图象如右图
的图象如右图
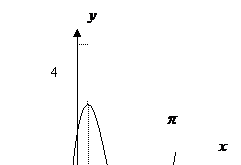 (Ⅰ)求
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)说明 的图象是由
的图象是由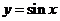 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
解: ( 1) 由图知A= 4
由 ,得
,得 所以
所以 由
由  ,得
,得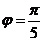
所以,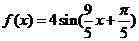
(2) ①由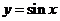 得图象向左平移
得图象向左平移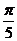 单位得
单位得 的图象
的图象
②
再由 图象的横坐标缩短为原来
图象的横坐标缩短为原来 得
得 的图象
的图象
③由 的图象纵坐标伸长为原来的4倍得
的图象纵坐标伸长为原来的4倍得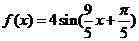 的图象
的图象
综合拔高训练
4.若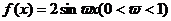 在区间
在区间 上的最大值是
上的最大值是 ,则
,则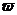 =________
=________
解析:

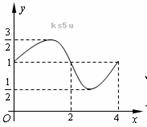
3. 函数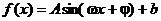 的图象如图,则
的图象如图,则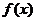 的解析式和
的解析式和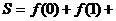
 的值分别为( )
的值分别为( )
 A.
A.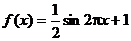 ,
, 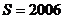
B.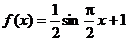 ,
, 
C.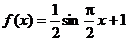 ,
, 
D.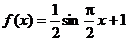 ,
, 
解析:B 观察图形知,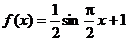 ,只知
,只知 ,
, ,
, ,
, ,
,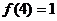 ,且以4为周期,
,且以4为周期, ,
,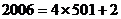 ,
,
∴
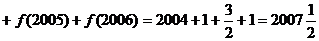 .
.
2.函数 是
是 上的偶函数,则
上的偶函数,则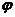 的值是( )
的值是( )
A
 B
B
 C
C
 D
D

解析:C 当 时,
时,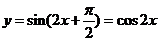 ,而
,而 是偶函数
是偶函数
1.(广东省六校2009届高三第二次联考试)将函数 的图象先向左平移
的图象先向左平移 ,然后将所得图象上所有的点的横坐标变为原来的
,然后将所得图象上所有的点的横坐标变为原来的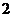 倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
A. B.
B.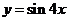 C.
C.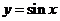 D.
D.
解析:将函数 的图象先向左平移
的图象先向左平移
得 ,然后将所得图象上所有的点的横坐标变为原来的
,然后将所得图象上所有的点的横坐标变为原来的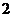 倍得
倍得 选C
选C
7.已知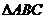 中,
中,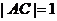 ,
, ,
,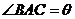 ,
,
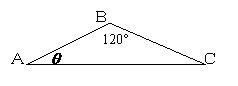 记
记 ,
,
(1)求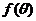 关于
关于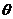 的表达式;
的表达式;
(2)求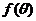 的值域;
的值域;
解:(1)由正弦定理有: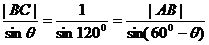 ;
;
∴ ,
, ;
;
∴
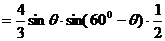


(2)由 ;
;
∴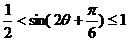 ;∴
;∴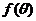
★抢 分 频 道
基础巩固训练
6.某港口的水深 (米)是时间
(米)是时间 (0≤
(0≤ ≤24,单位:小时)的函数,下面是不同时间的水深数据:
≤24,单位:小时)的函数,下面是不同时间的水深数据:

 根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成正弦函数
根据上述数据描出的曲线如图所示,经拟合,该曲线可近似地看成正弦函数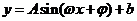 的图像.
的图像.
(1)试根据以上数据,求出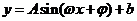 的表达式;
的表达式;
(2)一般情况下,船舶航行时,船底离海底的距离不少于4.5米时是安全的,如果某船的吃水深度(船底与水面的距离)为7米,那么该船在什么时间段能够安全进港?若该船欲当天安全离港,则在港内停留的时间最多不能超过多长时间?(忽略进出港所用的时间)?
[解析](1)从拟合曲线可知:函数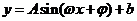 在一个周期内由最大变到最小需9-3=6小时,此为半个周期,所以函数的最小正周期为12小时,因此
在一个周期内由最大变到最小需9-3=6小时,此为半个周期,所以函数的最小正周期为12小时,因此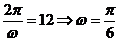 .
.
又当 时,
时, ;
; 时,
时, ;故
;故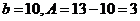
于是所求的函数表达式为了 .
.
(2)由于船的吃水深度为7米,船底与海底的距离不少于4.5米,故在船舶航行时水
深 应大于等于7+4.5=11.5(米).
应大于等于7+4.5=11.5(米).
令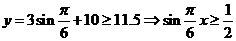
故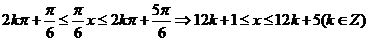
取 =0,则1≤
=0,则1≤ ≤5;取
≤5;取 =1,则13≤
=1,则13≤ ≤17;而取
≤17;而取 =2时,则25≤
=2时,则25≤ ≤29(不合题意).
≤29(不合题意).
从而可知船舶要在一天之内在港口停留时间最长,就应从凌晨1点(1点到5点都可以)进港,而下午的17点(即13点到17点之间)前离港,在港内停留的时间最长为16小时.
5.已知函数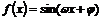 (
( ,
, )为偶函数,且其图像上相邻的一个最高点和最低点之间距离为
)为偶函数,且其图像上相邻的一个最高点和最低点之间距离为 .
.
⑴求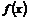 的解析式;
的解析式;
⑵若 ,求
,求 的值。
的值。
解析:⑴设最高点为 ,相邻的最低点为
,相邻的最低点为 ,则|x1–x2|=
,则|x1–x2|=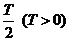
∴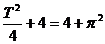 ,∴
,∴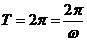 ,∴
,∴ ………………………(3分)
………………………(3分)
∴ , ∵
, ∵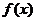 是偶函数,∴
是偶函数,∴ ,
, .
.
∵ ,∴
,∴ ,∴
,∴ …………… (6分)
…………… (6分)
⑵∵ ,∴
,∴ ………………………………(8分)
………………………………(8分)
∴原式
考点3 三角函数模型的简单应用
题型1. 形如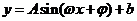 的建模
的建模
 [例1](2006·广东模拟)如图某地夏天从8-14时用电量变化曲线近似满足函数
[例1](2006·广东模拟)如图某地夏天从8-14时用电量变化曲线近似满足函数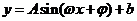 .
.
(1)求这一天的最大用电量及最小用电量;
(2)写出这段曲线的函数解析式.
[解题思路]在实际背景中抽取出基本的数学关系是解题的关键所在
[解析](1)最大用电量为50万度,最小用电量为30万度.
(2)观察图像可知,从8-14时的图像是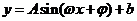 的半个周期的图像.
的半个周期的图像.
∴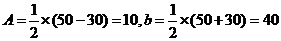 .
.
∵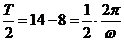 ,∴
,∴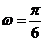 ,∴
,∴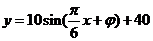
将 代入上式,解得
代入上式,解得
∴所求解析式为 .
.
[名师指引]①将实际问题抽象为与三角函数有关的简单函数模型.②利用收集到的数据作出散点图,并根据散点图进行函数拟合,从而得到函数模型.
题型2. 分析平面图形建立三角函数模型
[例2]如图, 是单位圆与
是单位圆与 轴正半轴的交点,点
轴正半轴的交点,点 在单位圆上,
在单位圆上, 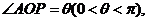

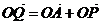 ,四边形
,四边形 的面积为
的面积为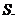
(Ⅰ)求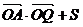 的最大值及此时
的最大值及此时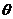 的值
的值 ;
;
(Ⅱ)设点 的坐标为
的坐标为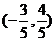 ,
, ,
,
在(Ⅰ)的条件下,求
[解题思路]由单位圆联想到三角函数的定义
解析:(Ⅰ)由已知, ,
, 的坐标分别为
的坐标分别为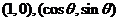
 ,
,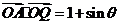
又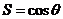
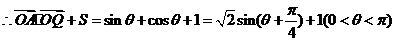
故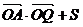 的最大值的最大值是
的最大值的最大值是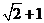 ,此时
,此时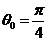
(Ⅱ)

[名师指引]分析实际问题时,若发现变量既与长度有关又与角度有关时,可考虑将变量设成角度.
题型3.利用三角与函数综合知识建立模型
例3.  如图,某小区准备在一直角围墙
如图,某小区准备在一直角围墙 内的空地上植造一块“绿地
内的空地上植造一块“绿地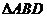 ”,其中
”,其中 长为定值
长为定值 ,
,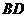 长可根据需要进行调节(
长可根据需要进行调节(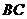 足够长).现规划在
足够长).现规划在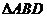 的内接正方形
的内接正方形 内种花,其余地方种草,且把种草的面积
内种花,其余地方种草,且把种草的面积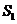 与种花的面积
与种花的面积 的比值
的比值 称为“草花比
称为“草花比 ”.
”.
(Ⅰ)设 ,将
,将 表示成
表示成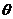 的函数关系式;
的函数关系式;
(Ⅱ)当 为多长时,
为多长时, 有最小值?最小值是多少?
有最小值?最小值是多少?
[解题思路]由条件知需找到边与角的关系,分析图形建模.
解:(Ⅰ)因为 ,所以
,所以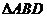 的面积为
的面积为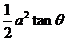 (
( ) 设正方形
) 设正方形 的边长为
的边长为 ,则由
,则由 ,得
,得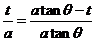 ,
,
解得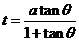 ,则
,则
所以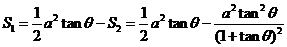 ,则
,则 (Ⅱ)因为
(Ⅱ)因为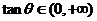 ,所以
,所以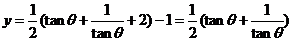
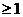 当且仅当
当且仅当 时取等号,此时
时取等号,此时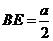 .所以当
.所以当 长为
长为 时,
时, 有最小值1
有最小值1
[名师指引]三角与函数综合知识建立模型是近两年高考的热点题型之一.
[新题导练]
4.若函数 的图像(部分)如下图所示,则
的图像(部分)如下图所示,则 和
和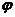 的取值是( )
的取值是( )
A、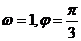 B、
B、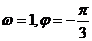 C、
C、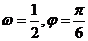 D、
D、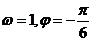

解析.C [由 解出即可]
解出即可]
3.函数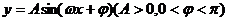 的图像的两个相邻零点为
的图像的两个相邻零点为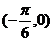 和
和
 ,且该函数的最大值为2,最小值为-2,则该函数的解析式为( )
,且该函数的最大值为2,最小值为-2,则该函数的解析式为( )
A、 B、
B、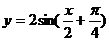
C、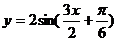 D、
D、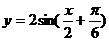
解析A. [由图像的两个相邻零点为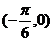 和
和 得
得
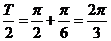
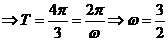 ,由最大值为2,最小值为-2知
,由最大值为2,最小值为-2知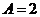 ,又函数过点
,又函数过点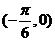 得
得 ,故
,故 ,而
,而 ,故
,故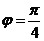 ,从而所求函数为
,从而所求函数为 ]
]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com