
题目列表(包括答案和解析)
7.(07年安徽)定义在R上的函数 既是奇函数,又是周期函数,
既是奇函数,又是周期函数, 是它的一个正周期.若将方程
是它的一个正周期.若将方程 在闭区间
在闭区间 上的根的个数记为
上的根的个数记为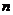 ,则
,则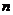 可能为( )
可能为( )
A.0;B.1;C.3;D.5
[解析] D;特取 ,
, ,则
,则 在
在 上的根有5个。
上的根有5个。
6.(08年陕西)为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为
 (
( ),传输信息为
),传输信息为 ,其中
,其中 ,
, 运算规则为:
运算规则为: ,
, ,
, ,
, ,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )
,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( )
A.11010;B.01100;C.10111;D.00011
[解析]C;假设传输信息为“10111”,那么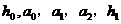 的值分别为“1,0,1,1,1”这5个数,据题目条件必有
的值分别为“1,0,1,1,1”这5个数,据题目条件必有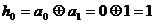 ;
;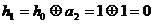 ,这与
,这与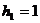 矛盾,故此信息错误。
矛盾,故此信息错误。
5. (恩城中学09届高三上中段考)已知定义在正整数集上的函数 满足条件:
满足条件: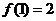 ,
,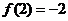 ,
,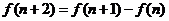 ,则
,则 的值为( )
的值为( )
A.-2;B.2;C.4;D.-4
[解析] B;由 的定义知,
的定义知, 是定义在正整数集上的周期为6的函数,故
是定义在正整数集上的周期为6的函数,故
4. 下列判断正确的是( )
A.函数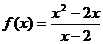 是奇函数;B.函数
是奇函数;B.函数 是偶函数
是偶函数
C.函数 是非奇非偶函数 D.函数
是非奇非偶函数 D.函数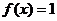 既是奇函数又是偶函数
既是奇函数又是偶函数
[解析] C;显然,函数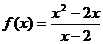 的定义域为
的定义域为 ,不关于原点对称,故排除A;函数
,不关于原点对称,故排除A;函数 的定义域为
的定义域为 也不关于原点对称,故排除B;又函数
也不关于原点对称,故排除B;又函数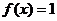 不是奇函数,所以应选择C
不是奇函数,所以应选择C
3.(09年重庆南开中学)已知集合 ,则集合N的真子集个数为( )
,则集合N的真子集个数为( )
A.3;B.4;C.7;D.8
[解析]B;由题意得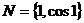 ,所以N的真子集个数为4
,所以N的真子集个数为4
2.(09年山东梁山二中)若 则实数
则实数 的取值范围是( )
的取值范围是( )
A.  ;B.
;B.  ;C.
;C.  ;D.
;D. 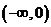
[解析] B;由题意知,集合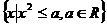 不是空集,故实数
不是空集,故实数 即其取值范围是
即其取值范围是
1.集合 ,
, ,则下列关系中,正确的是( )
,则下列关系中,正确的是( )
A.

 ;B.
;B.

 ;C.
;C.  ;D.
;D. 
[解析] D;由集合 的定义知,应选D(注意:本题易错选C)
的定义知,应选D(注意:本题易错选C)
8.如图所示的等腰梯形是一个简易水槽的横断面,已知水槽的最大流量与横断面的面积成正比,比例系数为 (
( ).
).
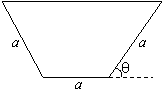 (Ⅰ)试将水槽的最大流量表示成关于
(Ⅰ)试将水槽的最大流量表示成关于 函数
函数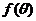 ;
;
(Ⅱ)求当 多大时,水槽的最大流量最大.
多大时,水槽的最大流量最大.
解:(1)设水槽的截面面积为S,则S=
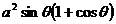
则
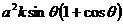 ,
,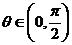 。
。
(2)因为 =
=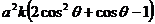 ,令
,令 =0,
=0,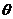 则2
则2 +
+ -1=0,
-1=0,
解得 =
=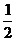 或
或 =-1。
=-1。
由于0<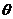 <
< ,得
,得
 -1,所以
-1,所以 =
=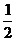 ,此时
,此时
因为0<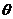 <
< 时,
时, >0;
>0; <
<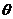 <
< 时,
时, <0;
<0;
所以,当 时,水槽的流量最大。
时,水槽的流量最大。
7.已知矩形纸片ABCD中,AB=6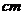 ,AD=12
,AD=12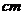 ,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点,M、N分别位于边AB、BC上,设
,将矩形纸片的右下角折起,使该角的顶点B落在矩形的边AD上,且折痕MN的两端点,M、N分别位于边AB、BC上,设 。
。
 (ⅰ)试将
(ⅰ)试将 表示成
表示成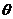 的函数;
的函数;
(ⅱ)求 的最小值。
的最小值。
如图所示,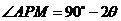 ,则MB=
,则MB= ,
, …
…
由题设得: +
+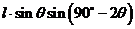 =6从而得
=6从而得 ……
……
即 ,
,
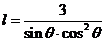 ……………
……………
设: 则
则 ,即
,即 ,
, ,
, 令
令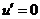 ,得
,得
当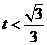 时,
时, ,当
,当 时,
时, ,所以当
,所以当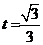 时,
时, 取到最大值:
取到最大值:
 的最小值为
的最小值为 ………………………………………
………………………………………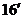
6.已知存在实数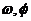 (其中
(其中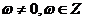 )使得函数
)使得函数 是奇函数,且在
是奇函数,且在 上是增函数。
上是增函数。
(1)试用观察法猜出两组 与
与 的值,并验证其符合题意;
的值,并验证其符合题意;
(2)求出所有符合题意的 与
与 的值。
的值。
解:(1)猜想: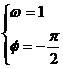 或
或 ;---------------------4分
;---------------------4分
由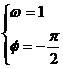 知
知 ,而
,而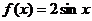 为奇函数且在
为奇函数且在 上是增函数。--------------------------------------6分
上是增函数。--------------------------------------6分
由 知
知 ,而
,而 为奇函数且在
为奇函数且在 上是增函数。----------------------------8分
上是增函数。----------------------------8分
(2)由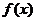 为奇函数,有
为奇函数,有
所以 ,又
,又 ,
,
解得 。-----------------------------------------------------10分
。-----------------------------------------------------10分
当 时,
时, 为奇函数,由于
为奇函数,由于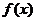 在
在 上是增函数,所以
上是增函数,所以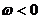 ,由
,由 ,又
,又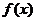 在
在 上是增函数,故有
上是增函数,故有 ,且
,且 或
或 ,故
,故 。----------------------------------------------------------12分
。----------------------------------------------------------12分
当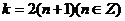 时,
时, 为奇函数,由于
为奇函数,由于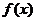 在
在 上是增函数,所以
上是增函数,所以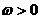 ,由
,由 ,又
,又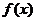 在
在 上是增函数,故有
上是增函数,故有 ,且
,且 或2,故
或2,故 --------------------------------------14分
--------------------------------------14分
所以所有符合题意的 与
与 的值为:
的值为:
 或
或 --------------------------------------16分
--------------------------------------16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com