6．若P＝+，Q＝+(a≥0)，则P、Q的大小关系是(　)

A．P＞Q 　　　　　　　　　 B．P＝Q

C．P＜Q　 　　　　　　　　 D．由a的取值确定

解析：假设P<Q，∵要证P＜Q，只要证P²＜Q²，

只要证：2a+7+2＜2a+7+2，

只要证：a²+7a＜a²+7a+12，

只要证：0＜12，

∵0＜12成立，∴P＜Q成立．

答案：C

5．若a＞b＞0，则下列不等式中总成立的是(　)

A．a+＞b+　 　　　　　　　　　　 B.＞

C．a+＞b+　 　　　　　　　　　　 D.＞

解析：∵a＞b＞0，∴＞.

又a＞b，∴a+＞b+.

答案：A

4．要证：a²+b²－1－a²b²≤0，只要证明(　)

A．2ab－1－a²b²≤0　 　　　　　　　　　　　　　 B．a²+b²－1－≤0

C.－1－a²b²≤0 　　　　　　 　　　 D．(a²－1)(b²－1)≥0

解析：因为a²+b²－1－a²b²≤0⇔(a²－1)(b²－1)≥0.

答案：D

3．设a，b，c∈(－∞，0)，则a+，b+，c+(　)

A．都不大于－2　 　　　　　　　　　　　　　 B．都不小于－2

C．至少有一个不大于－2　 　　　　　 D．至少有一个不小于－2

解析：因为a++b++c+≤－6，所以三者不能都大于－2.

答案：C

2．设a，b∈R，则“a+b＝1”是“4ab≤1”的(　)

A．充分不必要条件　 　　　　　　　　　　 B．必要不充分条件

C．充要条件　 　　　　　　　　　　　　 D．既不充分也不必要条件

解析：若“a+b＝1”，则4ab＝4a(1－a)＝－4(a－)²+1≤1；若“4ab≤1”，取a＝－4，b＝1，a+b＝－3，即“a+b＝1”不成立；则“a+b＝1”是“4ab≤1”的充分不必要条件．

答案：A

1．命题“对于任意角θ，cos⁴θ－sin⁴θ＝cos2θ”的证明：“cos⁴θ－sin⁴θ＝(cos²θ－sin²θ)(cos²θ+sin²θ)＝cos²θ－sin²θ＝cos2θ”过程应用了(　)

A．分析法　　　　　　　　　　　　　　　　　 B．综合法

C．综合法、分析法综合使用　 　　　　　　　　　　　　　 D．间接证明法

解析：因为证明过程是“从左往右”，即由条件⇒结论．

答案：B

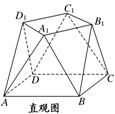
12．(2010·广东六校)一个多面体的直观图、正(主)视图、侧(左)视图如图(1)和(2)所示，其中正(主)视图、侧(左)视图均为边长为a的正方形．

(1)请在图(2)指定的位置画出多面体的俯视图；

(2)若多面体底面对角线AC、BD交于点O，E为线段AA₁的中点，求证：OE∥平面A₁C₁C；

图1

(3)求该多面体的表面积．

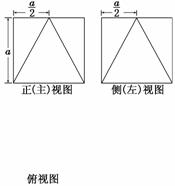
图2

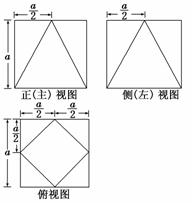解：(1)

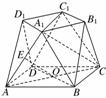
(2)证明：如图，连结AC、BD，交于O点．

∵E为AA₁的中点，O为AC的中点．

∴在△AA₁C中，OE为△AA₁C的中位线，

∴OE∥A₁C.

∵OE⊄平面A₁C₁C，A₁C⊂平面A₁C₁C，

∴OE∥平面A₁C₁C.

(3)多面体表面共包括10个面，S_ABCD＝a²，

S＝，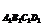

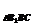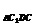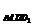S＝S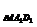＝S＝S＝，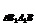

S＝S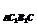＝S＝S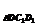

＝××＝，

所以该多面体的表面积S＝a²++4×+4×＝5a².

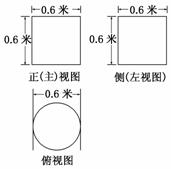
11．(2010·上海高考)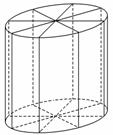如图所示，为了制作一个圆柱形灯笼，先要制作4个全等的矩形骨架，总计耗用9.6米铁丝．再用S平方米塑料片制成圆柱的侧面和下底面(不安装上底面)．

(1)当圆柱底面半径r取何值时，S取得最大值？并求出该最大值(结果精确到0.01平方米)；

(2)若要制作一个如图放置的、底面半径为0.3米的灯笼，请作出用于制作灯笼的三视图(作图时，不需考虑骨架等因素)．

解：(1)设圆柱的高为h，由题意可知，

4(4r+2h)＝9.6，

即2r+h＝1.2.

S＝2πrh+πr²

＝πr(2.4－3r)

＝3π[－(r－0.4)²+0.16]，其中0<r<0.6.

∴当半径r＝0.4(米)时，S_max＝0.48π≈1.51(平方米)．

(2)由r＝0.3及2r+h＝1.2，得圆柱的高h＝0.6(米)．则用于制作灯笼的三视图为：

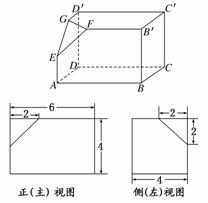
10．(2010·青岛质检)如下的三个图中，上面的是一个长方体截去一个角所得多面体的直观图，它的正(主)视图和侧(左)视图在下面画出(单位：cm)．

(1)在正(主)视图下面，按照画三视图的要求画出该多面体的俯视图；

(2)按照给出的尺寸，求该多面体的体积；

解：(1)如图．

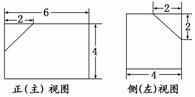
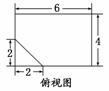
(2)所求多面体的体积

V＝V_长方体－V_正三棱锥＝4×4×6－××2

＝(cm³)．

9．如图是由大小相同的长方体木块堆成的几何体的三视图，则此几何体共由________块木块堆成．

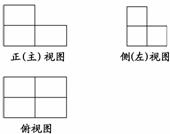
解析：根据题意可知，几何体的最底层有4块长方体，第2层有1块长方体，一共有5块．

答案：5